第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
5.阅读下列材料:
因式分解:$(x + y)^{2}+2(x + y)+1$.
解:将“$x + y$”看成整体,令$x + y = A$,
则原式$=A^{2}+2A + 1=(A + 1)^{2}$,
再将“$A$”还原,得原式$=(x + y + 1)^{2}$.
上述解题过程用到了“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题.
(1)因式分解:$9 + 6(x - y)+(x - y)^{2}=$_______.
(2)因式分解:$(a + b)(a + b - 8)+16$.
(3)证明:若$n$为正整数,则式子$(n + 1)(n + 2)(n + 3)(n + 4)+1$的值一定是某一个整数的平方.
因式分解:$(x + y)^{2}+2(x + y)+1$.
解:将“$x + y$”看成整体,令$x + y = A$,
则原式$=A^{2}+2A + 1=(A + 1)^{2}$,
再将“$A$”还原,得原式$=(x + y + 1)^{2}$.
上述解题过程用到了“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题.
(1)因式分解:$9 + 6(x - y)+(x - y)^{2}=$_______.
(2)因式分解:$(a + b)(a + b - 8)+16$.
(3)证明:若$n$为正整数,则式子$(n + 1)(n + 2)(n + 3)(n + 4)+1$的值一定是某一个整数的平方.
答案:
解析(1)将“x - y”看成整体,令 x - y = A,则原式 = A² + 6A + 9 = (A + 3)²,再将“A”还原,得原式 = (x - y + 3)²。故答案为(x - y + 3)²。(2)将“a + b”看成整体,令 a + b = A,则原式 = A(A - 8) + 16 = A² - 8A + 16 = (A - 4)²,再将“A”还原,得原式 = (a + b - 4)²。(3)证明:(n + 1)(n + 2)(n + 3)(n + 4) + 1= [(n + 1)(n + 4)]·[(n + 2)(n + 3)] + 1= (n² + 5n + 4)(n² + 5n + 6) + 1,令 n² + 5n = A,则原式 = (A + 4)(A + 6) + 1= A² + 10A + 25= (A + 5)²= (n² + 5n + 5)²,
∵ n 为正整数,
∴ n² + 5n + 5 是整数,
∴ 式子(n + 1)(n + 2)(n + 3)(n + 4) + 1 的值一定是某一个整数的平方。
∵ n 为正整数,
∴ n² + 5n + 5 是整数,
∴ 式子(n + 1)(n + 2)(n + 3)(n + 4) + 1 的值一定是某一个整数的平方。
6.新考向·项目学习试题(2023 湖南永州宁远期中)
提出问题:
你能把多项式$x^{2}+5x + 6$因式分解吗?
探究问题:
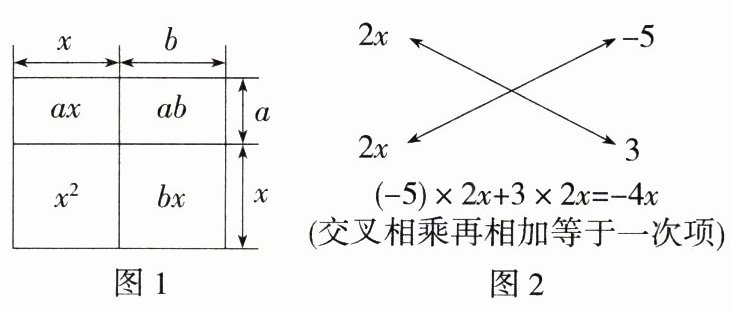
如图 1 所示,已知$a$,$b$为常数,由面积相等可得$(x + a)(x + b)=x^{2}+ax + bx + ab=x^{2}+(a + b)x + ab$,将该式从右到左使用,就可以对形如$x^{2}+(a + b)x + ab$的多项式进行因式分解,即$x^{2}+(a + b)x + ab=(x + a)(x + b)$.观察发现多项式$x^{2}+(a + b)x + ab$的特征是二次项系数为 1,常数项为两数之积,一次项系数为这两数之和.
解决问题:
$x^{2}+5x + 6=x^{2}+(2 + 3)x + 2×3=(x + 3)(x + 2)$.
运用结论:
(1)基础运用:对多项式$x^{2}-5x - 24$进行因式分解.
(2)知识迁移:对多项式$4x^{2}-4x - 15$进行因式分解时可以这样思考:将二次项$4x^{2}$分解成图 2 中的两个$2x$的积,再将常数项$-15$分解成$-5$与 3 的乘积,图中的对角线上的乘积的和为$-4x$,就是$4x^{2}-4x - 15$的一次项,所以有$4x^{2}-4x - 15=(2x - 5)(2x + 3)$,这种分解因式的方法叫作“十字相乘法”.请用“十字相乘法”进行因式分解:$3x^{2}-19x - 14$.
提出问题:
你能把多项式$x^{2}+5x + 6$因式分解吗?
探究问题:
如图 1 所示,已知$a$,$b$为常数,由面积相等可得$(x + a)(x + b)=x^{2}+ax + bx + ab=x^{2}+(a + b)x + ab$,将该式从右到左使用,就可以对形如$x^{2}+(a + b)x + ab$的多项式进行因式分解,即$x^{2}+(a + b)x + ab=(x + a)(x + b)$.观察发现多项式$x^{2}+(a + b)x + ab$的特征是二次项系数为 1,常数项为两数之积,一次项系数为这两数之和.
解决问题:
$x^{2}+5x + 6=x^{2}+(2 + 3)x + 2×3=(x + 3)(x + 2)$.
运用结论:
(1)基础运用:对多项式$x^{2}-5x - 24$进行因式分解.
(2)知识迁移:对多项式$4x^{2}-4x - 15$进行因式分解时可以这样思考:将二次项$4x^{2}$分解成图 2 中的两个$2x$的积,再将常数项$-15$分解成$-5$与 3 的乘积,图中的对角线上的乘积的和为$-4x$,就是$4x^{2}-4x - 15$的一次项,所以有$4x^{2}-4x - 15=(2x - 5)(2x + 3)$,这种分解因式的方法叫作“十字相乘法”.请用“十字相乘法”进行因式分解:$3x^{2}-19x - 14$.

答案:
解析(1)x² - 5x - 24 = x² + (3 - 8)x + 3×(-8)= (x + 3)(x - 8)。(2)用十字相乘法进行因式分解,如图,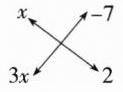
3x² - 19x - 14 = (x - 7)(3x + 2)。
解析(1)x² - 5x - 24 = x² + (3 - 8)x + 3×(-8)= (x + 3)(x - 8)。(2)用十字相乘法进行因式分解,如图,

3x² - 19x - 14 = (x - 7)(3x + 2)。
查看更多完整答案,请扫码查看


