《2025年5年中考3年模拟七年级数学下册青岛版》

8. (2024山东潍坊潍城期中改编)某校预安排若干间宿舍给七年级男寄宿生住，若每间宿舍住6人，则有4人住不下，若每间宿舍住7人，则有1间只住2人且空余8间宿舍. 问该校七年级男寄宿生有多少人? 预安排给七年级男寄宿生的宿舍有多少间?

答案： 解析 设该校七年级男寄宿生有x人，预安排给七年级男寄宿生的宿舍有y间， 根据题意，可列方程组为$\begin{cases}6y + 4 = x\\7(y - 8 - 1) + 2 = x\end{cases}$。 解得$\begin{cases}x = 394\\y = 65\end{cases}$。 答：该校七年级男寄宿生有394人，预安排给七年级男寄宿生的宿舍有65间。

9. 小颖家到学校的距离为1 200米，其中有一段为上坡路，另一段为下坡路，她去学校共用时16分钟，假设小颖在上坡路的平均速度为3千米/小时，下坡路的平均速度为5千米/小时，小颖家到学校的上坡路和下坡路各有多少米?

答案： 解析 设小颖家到学校的上坡路有x千米，下坡路有y千米。 根据题意可列方程为$\begin{cases}x + y = 1.2\\\frac{x}{3}+\frac{y}{5}=\frac{16}{60}\end{cases}$，解得$\begin{cases}x = 0.2\\y = 1\end{cases}$， 0.2千米 = 200米，1千米 = 1000米。 答：小颖家到学校的上坡路有200米，下坡路有1000米。

10. 甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按55%的利润定价，乙服装按45%的利润定价. 在实际出售时，应顾客要求，两件服装均按八折出售，这样商店共获利104元，问甲、乙两件服装的成本各是多少元? (M7209002)

答案： 解析 设甲服装的成本是x元，乙服装的成本是y元， 根据题意得$\begin{cases}x + y = 500\\x(1 + 55\%)×0.8 + y(1 + 45\%)×0.8 - x - y = 104\end{cases}$， 解得$\begin{cases}x = 300\\y = 200\end{cases}$。 答：甲服装的成本是300元，乙服装的成本是200元。

11. 巴川河是铜梁的母亲河，为打造巴川河风光带，现有一段长为360米的河道整治任务由A、B两个工程队先后接力完成. A工程队每天整治24米，B工程队每天整治16米，共用时20天.
(1)求A、B两工程队分别整治河道多少天. (用二元一次方程组解答)
(2)若A工程队整治一米的工费为200元，B工程队整治一米的工费为150元，求完成整治任务时，这两个工程队的工费共是多少元.

答案： 解析
(1)设A工程队整治河道x天，B工程队整治河道y天， 根据题意得$\begin{cases}x + y = 20\\24x + 16y = 360\end{cases}$，解得$\begin{cases}x = 5\\y = 15\end{cases}$。 答：A工程队整治河道5天，B工程队整治河道15天。
(2)根据题意得$200×24×5 + 150×16×15$ $= 24000 + 36000 = 60000$(元)。 答：完成整治任务时，这两个工程队的工费共是60000元。

12. (2024天津中考,9,★★☆)《孙子算经》是我国古代著名的数学典籍，其中有一道题:“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是:用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺. 问木长多少尺? 设木长x尺，绳子长y尺，则可以列出的方程组为(M7209002) ( )
A. $\begin{cases}y - x = 4.5 \\ x - 0.5y = 1\end{cases}$
B. $\begin{cases}y - x = 4.5 \\ x + 0.5y = 1\end{cases}$
C. $\begin{cases}x + y = 4.5 \\ x - y = 1\end{cases}$
D. $\begin{cases}x + y = 4.5 \\ y - x = 1\end{cases}$

答案： A
∵用绳子去量长木，绳子还剩余4.5尺，
∴$y - x = 4.5$。
∵将绳子对折再量长木，长木还剩余1尺，
∴$x - 0.5y = 1$。
∴可列方程组为$\begin{cases}y - x = 4.5\\x - 0.5y = 1\end{cases}$，故选A。

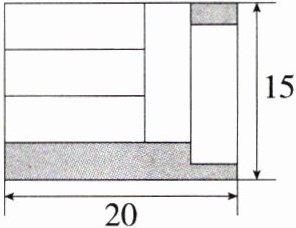
13. 数形结合思想 (2024云南昆明五华期末,14,★★☆)如图，在长为20，宽为15的大长方形中，有形状、大小完全相同的5个小长方形，若求阴影部分的面积，则应先求一个小长方形的面积，设小长方形的长为x，宽为y，根据题意，下列方程组正确的是 ( )

A. $\begin{cases}x + 2y = 20 \\ 4x = 15\end{cases}$
B. $\begin{cases}x + 2y = 20 \\ 4y = 15\end{cases}$
C. $\begin{cases}x + 2y = 20 \\ 3y = x\end{cases}$
D. $\begin{cases}x + 2y = 20 \\ x + y = 15\end{cases}$

答案： C
∵大长方形的长为20，
∴$x + 2y = 20$。观察题图可知$x = 3y$，
∴根据题意可列方程组为$\begin{cases}x + 2y = 20\\3y = x\end{cases}$，故选C。