《2025年5年中考3年模拟七年级数学下册青岛版》

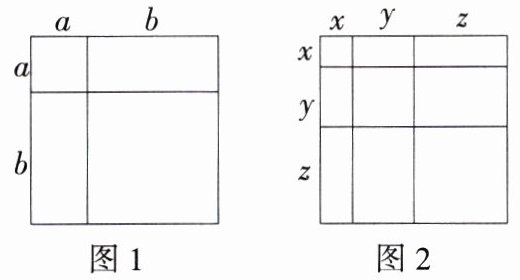
13.（2024山东青岛崂山实验学校月考，16，★☆☆）我们知道，多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性，如$(a + b)^{2}=a^{2}+2ab + b^{2}$就能利用图1的面积进行验证.那么，能利用图2的面积进行验证的含$x$、$y$、$z$的等式为__________.（M7210003）

答案： 答案：$(x + y+z)^2=x^2 + y^2+z^2+2xy + 2yz+2xz$ - 解析：题图2是边长为$x + y+z$的正方形，所以其面积为$(x + y+z)^2$， - 题图2的面积可表示为$x^2 + y^2+z^2+2xy + 2yz+2xz$， - 所以$(x + y+z)^2=x^2 + y^2+z^2+2xy + 2yz+2xz$.

14.（2022浙江温州瓯海期中改编，17，★☆☆）小冬以长方形$ABCD$的四条边为边向外作四个正方形，设计出“中”字图案，如图所示.若四个正方形的周长之和为48，面积之和为52，则长方形$ABCD$的面积为__________.（M7210003）

答案： 答案：5 - 解析：设$AB = a$，$BC = b$，由四个正方形的周长之和为48，面积之和为52，可得$4a\times2+4b\times2 = 48$，$2a^2+2b^2=52$，故$a + b = 6$，$a^2 + b^2=26$， - 所以$(a + b)^2=a^2+2ab + b^2=36$， - 所以$2ab = 36-26 = 10$，所以$ab = 5$. 故长方形ABCD的面积为5.

15.（2024陕西中考，15，★☆☆）先化简，再求值：$(x + y)^{2}+x(x - 2y)$，其中$x = 1$，$y=-2$.

答案： 解析 - 原式$=x^2+2xy + y^2+x^2-2xy=2x^2 + y^2$， - 当$x = 1$，$y=-2$时，原式$=2\times1^2+(-2)^2=6$.

16.（2024山东济南莱芜莲河学校月考，19，★☆☆）已知：$x + y = 3$，$xy=-2$，求下列代数式的值：
(1)$x^{2}+y^{2}$.
(2)$(x - y)^{2}$.

答案： 解析 -
(1)因为$x + y = 3$，$xy=-2$， - 所以$x^2 + y^2=(x + y)^2-2xy=3^2-2\times(-2)=9 + 4 = 13$. -
(2)因为$x + y = 3$，$xy=-2$，所以$(x + y)^2=9$， - 所以$(x - y)^2=(x + y)^2-4xy=9-4\times(-2)=9 + 8 = 17$.

17. 推理能力 发现：两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和.如$(2 + 1)^{2}+(2 - 1)^{2}=10$，10为偶数.请把10的一半表示为两个正整数的平方和，并验证发现中的结论.

答案： 解析 - 10的一半为5，$5 = 1 + 4=1^2+2^2$. - 验证结论如下： - 设两个已知正整数分别为m，n. - 因为$(m + n)^2+(m - n)^2=m^2+2mn + n^2+m^2-2mn + n^2=2m^2+2n^2=2(m^2 + n^2)$，所以$(m + n)^2+(m - n)^2$为偶数，且该偶数的一半可以表示为$m^2 + n^2$，故两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和.

18. 推理能力 新考向·项目式学习试题 （2024山东济南章丘期中）【知识生成】
通常情况下，通过用两种不同的方法计算同一个图形的面积，可以得到一个恒等式，如图①，从边长为$a$的长方形中剪掉一个边长为$b$的小正方形，将阴影部分沿虚线剪开拼成如图②所示的长方形.

(1)比较图①、图②的阴影部分面积，可以得到的乘法公式为______________.
如图③，可以验证的等式为____________________.（用字母$a$，$b$表示）
【问题探究】
(2)已知$a + b = 3$，$ab = 1$，求$a^{2}+b^{2}$的值.
【拓展计算】
(3)$(1-\frac{1}{2^{2}})\times(1-\frac{1}{3^{2}})\times(1-\frac{1}{4^{2}})\times\cdots\times(1-\frac{1}{2022^{2}})\times(1-\frac{1}{2023^{2}})$.

答案： 解析 -
(1)题图①中阴影部分面积可以看作两个正方形的面积差，即$a^2 - b^2$，拼成的题图②是长为$(a + b)$，宽为$(a - b)$的长方形， - 所以面积为$(a + b)(a - b)$， - 所以$(a + b)(a - b)=a^2 - b^2$， - 题图③整体上是边长为$(a + b)$的正方形，因此面积为$(a + b)^2$，组成题图③的四个部分的面积和为$S_1+S_2+S_3+S_4=a^2+ab + ab + b^2=a^2+2ab + b^2$， - 所以$(a + b)^2=a^2+2ab + b^2$. 故答案为$(a + b)(a - b)=a^2 - b^2$；$(a + b)^2=a^2+2ab + b^2$. -
(2)由题意得$(a + b)^2=3^2 = 9$，$2ab = 2\times1 = 2$， - 所以$a^2 + b^2=(a + b)^2-2ab=9-2 = 7$. -
(3)原式$=(1-\frac{1}{2})\times(1+\frac{1}{2})\times(1-\frac{1}{3})\times(1+\frac{1}{3})\times\cdots\times(1-\frac{1}{2023})\times(1+\frac{1}{2023})=\frac{1}{2}\times\frac{3}{2}\times\frac{2}{3}\times\frac{4}{3}\times\cdots\times\frac{2022}{2023}\times\frac{2024}{2023}=\frac{1}{2}\times\frac{2024}{2023}=\frac{1012}{2023}$.