第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
16.平行线+角平分线模型 (2024山东德州德城五月月考,22,★★☆)如图,△ABC中,CD平分∠ACB,DE//BC,交AC于点E.
(1)求证:∠1 = ∠2.
(2)若∠AED = 64°,求∠DCB的度数.
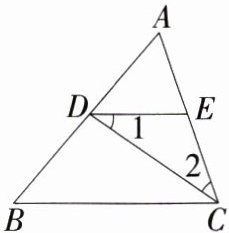
(1)求证:∠1 = ∠2.
(2)若∠AED = 64°,求∠DCB的度数.

答案:
解析 (1)证明:因为CD平分∠ACB,所以∠BCD = ∠2,因为DE//BC,所以∠BCD = ∠1,所以∠1 = ∠2。
(2)因为DE//BC,∠AED = 64°,所以∠ACB = ∠AED = 64°,因为CD平分∠ACB,所以∠DCB = $\frac{1}{2}$∠ACB = 32°。
17.推理能力 新考向·项目学习试题 (2024山东青岛城阳期末)【发现问题】
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
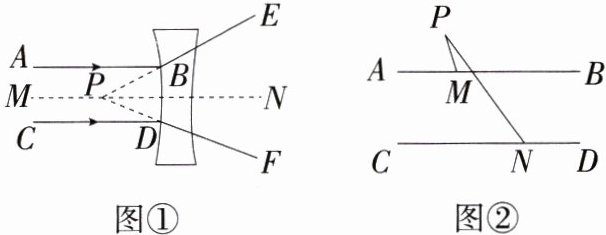
【提出问题】
小明提出:∠BPD,∠ABP和∠CDP之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
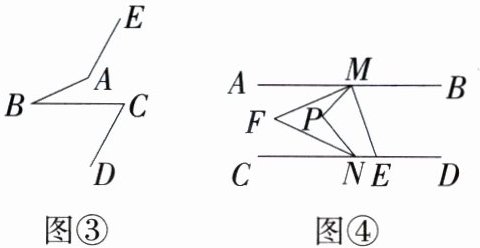
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为__________.
如图③,已知∠ABC = 25°,∠C = 60°,AE//CD,则∠BAE = __________°.(不需要写解答过程)
【拓展提升】
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P = 2∠F,求∠FME的度数.
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.


【提出问题】
小明提出:∠BPD,∠ABP和∠CDP之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为__________.
如图③,已知∠ABC = 25°,∠C = 60°,AE//CD,则∠BAE = __________°.(不需要写解答过程)
【拓展提升】
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P = 2∠F,求∠FME的度数.
答案:
解析 探究一:∠BPD = ∠ABP + ∠CDP,理由如下:因为AB//MN//CD,所以∠BPN = ∠ABP,∠DPN = ∠CDP,所以∠BPN + ∠DPN = ∠ABP + ∠CDP,所以∠BPD = ∠ABP + ∠CDP。
探究二:∠AMP = ∠P + ∠CNP;145。
详解:如图1,因为AB//CD,所以∠MKP = ∠CNP,因为∠P + ∠PKM + ∠PMK = 180°,∠PMK + ∠PMA = 180°,所以∠AMP = ∠P + ∠MKP,所以∠AMP = ∠P + ∠CNP。
如图2,延长EA交BC于L,因为AE//CD,所以∠ALC = ∠C = 60°,所以∠ALB = 180° - ∠ALC = 120°,因为∠BAL + ∠B + ∠ALB = 180°,所以∠BAL = 35°,所以∠BAE = 180° - 35° = 145°。
【拓展提升】因为射线ME,NF分别平分∠BMP和∠CNP,所以∠PME = $\frac{1}{2}$∠PMB,∠CNF = ∠PNF,由探究一的结论得∠P = ∠AMF + ∠PMF + ∠CNF + ∠PNF,∠F = ∠AMF + ∠CNF,因为∠P = 2∠F,所以∠AMF + ∠PMF + ∠CNF + ∠PNF = 2∠AMF + 2∠CNF,因为∠CNF = ∠PNF,所以∠AMF + ∠PMF = 2∠AMF,所以∠PMF = ∠AMF = $\frac{1}{2}$∠AMP,所以∠PMF + ∠PME = $\frac{1}{2}$(∠AMP + ∠PMB),所以∠FME = $\frac{1}{2}$∠AMB = $\frac{1}{2}$×180° = 90°。
查看更多完整答案,请扫码查看


