《2025年5年中考3年模拟七年级数学下册青岛版》

10.五条直线两两相交于同一点时，对顶角有m对，交于不同五点时，对顶角有n对，则m与n的关系是（M7208001） （ ）
A.m = n
B.m＞n
C.m＜n
D.m + n = 10

答案： A：因为五条直线两两相交形成的对顶角的对数与是否交于同一点无关，所以 m = n，故选 A.

11.（2023甘肃兰州中考）如图，直线AB与CD相交于点O，则∠BOD =（M7208001） （ ）

A.40°
B.50°
C.55°
D.60°

答案： B：
∵直线 AB 与 CD 相交于点 O，
∴∠BOD = ∠AOC，
∵∠AOC = 50°，
∴∠BOD = 50°.故选 B.

12.下列说法正确的有 （ ）
①对顶角相等；②互补的两个角是邻补角；
③若两个角不相等，则这两个角一定不是对顶角；④若两个角不是对顶角，则这两个角一定不相等.
A.1个
B.2个
C.3个
D.4个

答案： B：互为对顶角的两个角一定相等，因此，若两个角不相等，则它们一定不是对顶角，所以①③正确.对顶角强调位置关系，不是对顶角的两个角有可能相等，所以④错误.互为邻补角的两个角不仅和为 180°，而且有一条公共边，另一边互为反向延长线，所以不能只从数量关系上来判断，所以②错误.故正确的有 2 个.故选 B.

13.（2024广西中考）已知∠1与∠2为对顶角，∠1 = 35°，则∠2 = ______°.（M7208001）

答案： 答案：35 **解析**：
∵∠1 与∠2 为对顶角，∠1 = 35°，
∴∠2 = ∠1 = 35°.

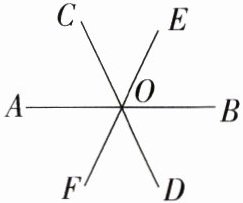
14.如图，AB，CD，EF相交于点O，∠AOC = 65°，∠DOF = 50°.（M7208001）
（1）求∠BOE的度数.
（2）计算∠AOF的度数，你能发现射线OA有什么特殊性吗？

答案： 解析： （1）因为∠AOC = 65°，所以∠BOD = ∠AOC = 65°.因为∠BOE + ∠BOD + ∠DOF = 180°，所以∠BOE = 180° - 65° - 50° = 65°. （2）由（1）知∠BOE = 65°，所以∠AOF = ∠BOE = 65°.因为∠AOC = 65°，所以∠AOF = ∠AOC，所以射线 OA 是∠COF 的平分线.

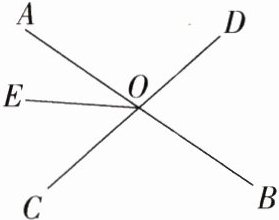
15.易错题（2023江苏苏州景城学校月考，18，★★☆）如图，直线AB、CD相交于点O.已知∠BOD = 75°，OE把∠AOC分成两个角，且∠AOE = $\frac{2}{3}$∠EOC，将射线OE绕点O逆时针旋转α（0°＜α＜360°）到OE'，若∠AOE' = 120°，则α的度数是____________.（M7208001）

答案： 答案：90°或 210° **解析**：OE 在运动过程中有两个位置可以使∠AOE' = 120°，分情况讨论. ①当 OE 运动到如图 1 所示的位置时，
∵∠BOD = 75°，
∴∠AOC = ∠BOD = 75°，
∵∠AOE = $\frac{2}{3}$∠EOC，
∴∠AOE = $\frac{2}{5}$∠AOC = $\frac{2}{5}$×75° = 30°， 又∠AOE' = 120°，
∴α = ∠AOE' - ∠AOE = 120° - 30° = 90°. ②当 OE 运动到如图 2 所示的位置时，
∵∠BOD = 75°，
∴∠AOC = ∠BOD = 75°，
∵∠AOE = $\frac{2}{3}$∠EOC，
∴∠AOE = $\frac{2}{5}$∠AOC = $\frac{2}{5}$×75° = 30°， 又∠AOE' = 120°，
∴α = 360° - (∠AOE' + ∠AOE) = 360° - 150° = 210°. 故答案为 90°或 210°.

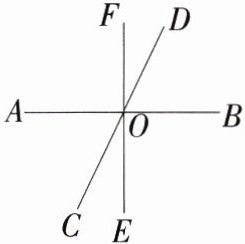
16.（2024甘肃定西岷县月考，25，★★☆）如图，直线AB，CD，EF相交于点O.
（1）分别写出∠COE的邻补角和∠BOE的对顶角.
（2）如果∠BOD = 60°，∠BOF = 90°，求∠FOC的度数.

答案： 解析： （1）∠COE 的邻补角为∠COF 和∠DOE，∠BOE 的对顶角为∠AOF. （2）
∵∠BOF = 90°，
∴∠AOF = 180° - ∠BOF = 180° - 90° = 90°，
∵∠AOC = ∠BOD = 60°，
∴∠FOC = ∠AOF + ∠AOC = 150°.

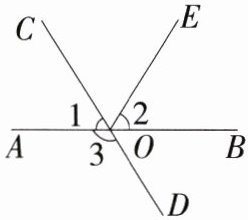
17.教材变式（2024河南商丘虞城月考，19，★★☆）如图，直线AB，CD相交于点O，∠3 - ∠2 = 65°.
（1）求∠COE的度数.
（2）若∠1 = ∠2，求∠3的度数.

答案： 解析： （1）
∵∠3 = ∠BOC，∠BOC = ∠COE + ∠2，
∴∠3 = ∠COE + ∠2，
∵∠3 - ∠2 = 65°，
∴∠COE = ∠3 - ∠2 = 65°. （2）由（1）知∠COE = 65°， ∠∠1 = ∠2，
∴∠1 = ∠2 = $\frac{180° - ∠COE}{2}$ = 57.5°，
∴∠3 = 180° - ∠1 = 122.5°.