《2025年5年中考3年模拟七年级数学下册青岛版》

1. (2024湖南郴州永兴树德中学月考)下列计算错误的是(M7210002) ( )
A. $(x + 1)(x + 3)=x^{2}+4x + 3$
B. $(x + 2)(x - 3)=x^{2}-x - 6$
C. $(x - 3)(x - 2)=x^{2}-5x + 6$
D. $(x - 5)(x + 1)=x^{2}-6x - 5$

答案： D：$(x - 5)(x + 1)=x^{2}-4x - 5$，故 D 错误，符合题意。

2. (2024江西九江都昌期中)计算$(a - 2)(-a + 1)$的结果是 ( )
A. $a^{2}-a - 2$
B. $-a^{2}-a - 2$
C. $-a^{2}+3a - 2$
D. $a^{2}+3a - 2$

答案： C：$(a - 2)(-a + 1)=-a^{2}+a + 2a - 2=-a^{2}+3a - 2$，故选 C。

3. (2024江苏扬州邗江期末)如图,长为$a$、宽为$b$的长方形的周长为12,面积为7,则$(a + 1)(b + 1)$的值为(M7210002) ( )

A. 14
B. 15
C. 16
D. 20

答案： A：因为长方形的长为$a$、宽为$b$，周长为$12$，面积为$7$，所以$2(a + b)=12$，$ab = 7$，则$a + b = 6$，所以$(a + 1)(b + 1)=ab + a + b + 1=7 + 6 + 1 = 14$，故选 A。

4. 计算：(M7210002)
(1) $(a + 3)(a - 1)+a(a - 2)$.
(2) $(y + 2)(y - 2)-(y - 1)(y + 5)$.

答案： 解析：\n（1）原式$=(a^{2}-a + 3a - 3)+(a^{2}-2a)=a^{2}+2a - 3+a^{2}-2a = 2a^{2}-3$。\n（2）原式$=(y^{2}-2y + 2y - 4)-(y^{2}+5y - y - 5)=y^{2}-4 - y^{2}-4y + 5=-4y + 1$。

5. 先化简,再求值：(M7210002)
(1) $(2x + 1)(x - 5)-(3x + 1)(5x - 2)$,其中$x = -1$.
(2) $(a + b)(a - 2b)+(a + 2b)(a - b)-2a^{2}$,其中$a = 3$, $b = -\frac{1}{3}$.

答案： 解析：\n（1）$(2x + 1)(x - 5)-(3x + 1)(5x - 2)=(2x^{2}-10x + x - 5)-(15x^{2}-6x + 5x - 2)=2x^{2}-9x - 5 - 15x^{2}+x + 2=-13x^{2}-8x - 3$，当$x = -1$时，原式$=-13×(-1)^{2}-8×(-1)-3=-13 + 8 - 3=-8$。\n（2）$(a + b)(a - 2b)+(a + 2b)(a - b)-2a^{2}=(a^{2}-2ab + ab - 2b^{2})+(a^{2}-ab + 2ab - 2b^{2})-2a^{2}=a^{2}-ab - 2b^{2}+a^{2}+ab - 2b^{2}-2a^{2}=-4b^{2}$，当$b = -\frac{1}{3}$时，原式$=-4×(-\frac{1}{3})^{2}=-\frac{4}{9}$。

6. [新考向·新定义试题]$\begin{vmatrix}a&b\\c&d\end{vmatrix}$被称为二阶行列式,它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$,如$\begin{vmatrix}2&-5\\3&4\end{vmatrix}=2\times4-(-5)\times3 = 23$.请你根据二阶行列式的运算法则化简$\begin{vmatrix}x&x - 1\\x + 3&x - 2\end{vmatrix}$. (M7210002)

答案： 解析：$\begin{vmatrix}x&x - 1\\x + 3&x - 2\end{vmatrix}=x(x - 2)-(x - 1)(x + 3)=x^{2}-2x-(x^{2}+3x - x - 3)=x^{2}-2x - x^{2}-3x + x + 3=-4x + 3$。

7. (2024山东济南莱芜期末,5,★☆☆)若$x - m$与$3x - 2$的乘积中不含$x$的一次项,则$m$的值为 ( )
A. $-\frac{2}{3}$
B. $-\frac{3}{2}$
C. $\frac{3}{2}$
D. 3

答案： A：$(x - m)(3x - 2)=3x^{2}-2x - 3mx + 2m=3x^{2}-(2 + 3m)x + 2m$，由题意得$-(2 + 3m)=0$，解得$m = -\frac{2}{3}$，故选 A。

8. (2024山东枣庄市中实验中学月考,9,★☆☆)用图中所示的正方形和长方形卡片若干张,拼成一个长为$3a + 2b$,宽为$2a + b$的长方形,则需要$A$类、$B$类、$C$类卡片的张数分别是(M7210002) ( )

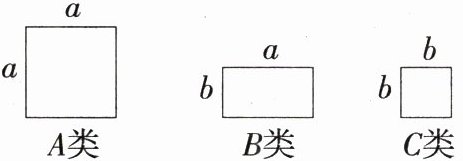
A. 5、6、2
B. 6、7、3
C. 6、7、2
D. 5、7、3

答案： C：因为长方形的长为$3a + 2b$，宽为$2a + b$，所以长方形的面积为$(3a + 2b)(2a + b)=6a^{2}+7ab + 2b^{2}$，所以需要 A 类、B 类、C 类卡片的张数分别是 6、7、2，故选 C。

9. [情境题·数学文化] (2024湖南岳阳期末,10,★☆☆)欧拉引进了求和符号“$\sum_{k = i}^{n}k$”(其中$i\leq n$,且$i$和$n$表示正整数),对这个符号我们进行如下定义：$\sum_{k = i}^{n}k$表示$k$从$i$开始取数一直取到$n$,全部加起来,即$\sum_{k = i}^{n}k=i+(i + 1)+(i + 2)+(i + 3)+\cdots +n$.例如：当$i = 1$时,$\sum_{k = 1}^{n}k = 1+2+3+4+\cdots +n$.若$\sum_{k = 2}^{n}(x - k)(x - k + 1)=3x^{2}+px + m$,则$p$、$m$表示的数分别为 ( )
A. $-6$、9
B. $-15$、20
C. 30、$-81$
D. 27、$-243$

答案： B：因为$\sum_{k = 2}^{n}(x - k)(x - k + 1)=3x^{2}+px + m$，且$3x^{2}+px + m$中二次项系数为 3，所以$n = 4$，所以$\sum_{k = 2}^{n}(x - k)(x - k + 1)=(x - 2)(x - 1)+(x - 3)(x - 2)+(x - 4)(x - 3)=x^{2}-x - 2x + 2+x^{2}-2x - 3x + 6+x^{2}-3x - 4x + 12=3x^{2}-15x + 20$，因为$\sum_{k = 2}^{n}(x - k)(x - k + 1)=3x^{2}+px + m$，所以$3x^{2}-15x + 20=3x^{2}+px + m$，所以$p = -15$，$m = 20$，故选 B。