《2025年5年中考3年模拟七年级数学下册青岛版》

10. [新考向·新定义试题] (2024山东青岛崂山期末,13,★☆☆)在综合与实践课上,小明设计了如下的运算：$a\otimes b=(ax + 2b)(bx - a)$,则$1\otimes2$经过运算可化简为________. (M7210002)

答案： 答案：$2x^{2}+7x - 4$ 解析：因为$a\otimes b=(ax + 2b)(bx - a)$，所以$1\otimes2=(x + 2×2)(2x - 1)=(x + 4)(2x - 1)=2x^{2}-x + 8x - 4=2x^{2}+7x - 4$。

11. (2024山东济南商河期中,15,★☆☆)若$(x - 1)(x + 3)=x^{2}+mx + n$,则$m + n =$________. (M7210002)

答案： 答案：$-1$ 解析：$(x - 1)(x + 3)=x^{2}+2x - 3=x^{2}+mx + n$，所以$m = 2$，$n = -3$，则$m + n=2 - 3=-1$。

12. (2024河南周口项城月考,21,★☆☆)小诚计算$(3x - 3a)(5x + a)$时,由于把第一个多项式中的“$-3a$”看成了“$+3a$”,得到的结果为$15x^{2}+12x+\frac{4}{3}$.
(1)求$a$的值.
(2)计算这道整式乘法的正确结果.

答案： 解析：（1）由题意得$(3x + 3a)(5x + a)=15x^{2}+12x+\frac{4}{3}$，所以$15x^{2}+15ax + 3ax + 3a^{2}=15x^{2}+12x+\frac{4}{3}$，所以$15x^{2}+18ax + 3a^{2}=15x^{2}+12x+\frac{4}{3}$，则$\begin{cases}18a = 12\\3a^{2}=\frac{4}{3}\end{cases}$，所以$a=\frac{2}{3}$。（2）$(3x - 3a)(5x + a)=15x^{2}-15ax + 3ax - 3a^{2}=15x^{2}-12ax - 3a^{2}$，当$a=\frac{2}{3}$时，原式$=15x^{2}-8x-\frac{4}{3}$。

13. (2024山东济南历下期中,23,★☆☆)如图所示的是人民公园的一块长为$(2m + n)$米,宽为$(m + 2n)$米的空地.计划在空地上建造一个观景台(阴影部分).
(1)请用$m$、$n$表示观景台的面积.(结果化为最简)
(2)如果修建观景台的费用为200元/平方米,且已知$m = 5$, $n = 4$,那么修建观景台需要的费用是多少元? (M7210002)

答案： 解析：\n（1）阴影部分的面积为$(2m + n)(m + 2n)-mn-(m - n)^{2}-(2m + n)(m - n)=2m^{2}+4mn + mn + 2n^{2}-mn-(m^{2}-2mn + n^{2})-(2m^{2}-2mn + mn - n^{2})=2m^{2}+4mn + mn + 2n^{2}-mn - m^{2}+2mn - n^{2}-2m^{2}+2mn - mn + n^{2}=-m^{2}+7mn + 2n^{2}$，所以观景台的面积为$(-m^{2}+7mn + 2n^{2})$平方米。\n（2）当$m = 5$，$n = 4$时，原式$=-25 + 7×5×4+2×16 = 147$，$200×147 = 29400$（元），所以修建观景台需要的费用为 29400 元。

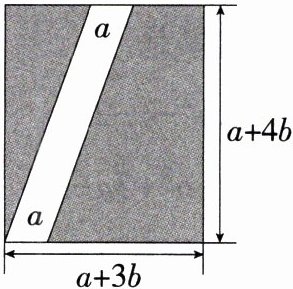
14. [情境题·劳动教育] (2024江苏扬州邗江期末,24,★☆☆)为了更好地开展劳动教育,某学校暑期对学校闲置的地块进行规划改造,已知该地块是长为$(a + 4b)$米,宽为$(a + 3b)$米的长方形地块(如图),学校准备在该地块内修一条平行四边形小路,小路的宽为$a$米,并计划将阴影部分改造为种植区. (M7210002)
(1)用含有$a$、$b$的式子分别表示出小路的面积$S_{1}$和种植区的总面积$S_{2}$. (请将结果化为最简)
(2)若$a = 2$, $b = 4$,求出此时种植区的总面积$S_{2}$.

答案： 解析：（1）$S_{1}=a(a + 4b)=(a^{2}+4ab)$平方米，$S_{2}=(a + 3b - a)(a + 4b)=3b(a + 4b)=(3ab + 12b^{2})$平方米。（2）当$a = 2$，$b = 4$时，$S_{2}=3×2×4+12×4^{2}=3×2×4+12×16 = 24 + 192 = 216$（平方米），答：种植区的总面积$S_{2}$为 216 平方米。

15. [运算能力] (2024山东菏泽鲁西新区期中)先观察下列各式,再解答后面的问题：$(x + 5)(x + 6)=x^{2}+11x + 30$, $(x - 5)(x - 6)=x^{2}-11x + 30$, $(x - 5)(x + 6)=x^{2}+x - 30$. (M7210002)
(1)等号右边中的一次项系数、常数项与等号左边两因式中的常数项有何关系?
(2)根据以上各式呈现的规律,用公式表示出来.
(3)试用你写的公式,直接写出下列两式的结果.
①$(a + 99)(a - 100)=$________.
②$(y - 500)(y - 81)=$________.

答案： 解析：（1）等号左边两因式中常数项的和等于等号右边中的一次项系数，常数项的积等于等号右边中的常数项。（2）$(x + a)(x + b)=x^{2}+(a + b)x + ab$。（3）①$(a + 99)(a - 100)=a^{2}-a - 9900$。②$(y - 500)(y - 81)=y^{2}-581y + 40500$。