《2025年5年中考3年模拟七年级数学下册青岛版》

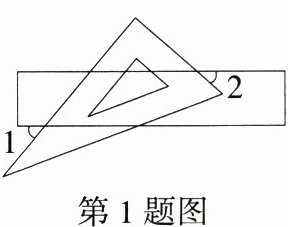
1.（2024 黑龙江齐齐哈尔中考改编）将一个含30°角的三角尺和一把直尺按如图所示的方式放置，若∠1 = 50°，则∠2的度数是（ ）

A.30°
B.40°
C.50°
D.60°

答案：
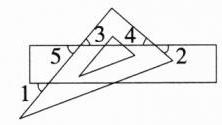
B 如图，
∵ 直尺的对边平行，
∴ ∠5 = ∠1 = 50°，
∴ ∠3 = ∠5 = 50°，
∴ ∠4 = 180° - 90° - ∠3 = 40°，
∴ ∠2 = ∠4 = 40°. 故选 B. 

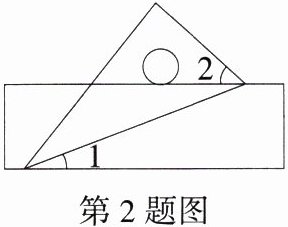
2.（2023 山东菏泽中考）将一把直尺和一个含30°角的直角三角尺按如图所示的方式放置，若∠1 = 20°，则∠2 =（ ）

A.30°
B.40°
C.50°
D.60°

答案：
B 如图，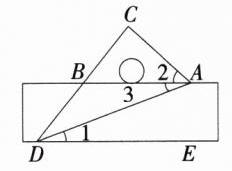
由题意得 ∠CAD = 60°，
∵ AB // DE，∠1 = 20°，
∴ ∠3 = ∠1 = 20°，
∴ ∠2 = ∠CAD - ∠3 = 40°. 故选 B.

3.（2023 湖北襄阳中考）将含有45°角的三角尺和直尺按如图所示的方式叠放在一起，若∠1 = 30°，则∠2的度数为（ ）

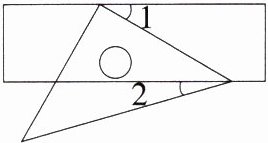
A.30°
B.20°
C.15°
D.10°

答案：
C 如图，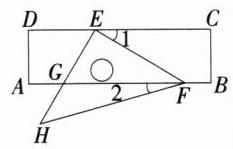
依题意得 AB // CD，∠EFH = 45°，
∴ ∠EFG = ∠1 = 30°，
∴ ∠2 = ∠EFH - ∠EFG = 45° - 30° = 15°. 故选 C.

4.（2023 内蒙古呼伦贝尔、兴安盟中考）将一副直角三角尺按如图所示的方式摆放，点C在FD的延长线上，且AB//FC，则∠CBD的度数为（ ）

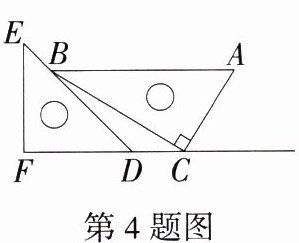
A.10°
B.15°
C.20°
D.25°

答案： B
∵ AB // FC，
∴ ∠ABD = ∠EDF = 45°，
∵ ∠CBD = ∠ABD - ∠ABC，
∴ ∠CBD = 45° - 30° = 15°，故选 B.

5.（2023 内蒙古通辽中考）将一副三角尺按如图所示的方式放置，其中AB//DE，则∠CDF = ________度.

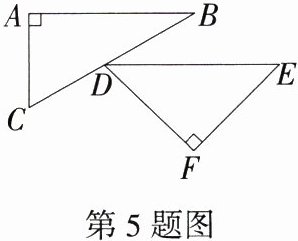
答案： 答案 105 解析
∵ AB // DE，
∴ ∠BDE = ∠B = 30°.
∴ ∠CDF = 180° - ∠EDF - ∠BDE = 180° - 45° - 30° = 105°. 故答案为 105.

6.（2024 山东泰安宁阳期中）如图，将长方形纸片ABCD沿EF折叠，A，D两点分别与A'，D'对应，若∠1 = 2∠2，则∠AEF的度数为（ ）

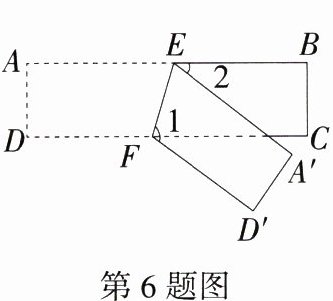
A.60°
B.65°
C.72°
D.75°

答案： C
∵ AB // DC，
∴ ∠1 = ∠AEF， 由折叠的性质得出 ∠AEF = ∠FEA'，
∵ ∠1 = 2∠2，
∴ ∠AEF = ∠FEA' = 2∠2，
∵ ∠AEF + ∠FEA' + ∠2 = 180°，
∴ 2∠2 + 2∠2 + ∠2 = 180°， 解得 ∠2 = 36°.
∴ ∠AEF = 72°. 故选 C.

7.（2024 福建龙岩长汀期中）如图，将△ADE沿直线DE折叠，使点A落在BC边上的点F处，DE//BC，若∠C = 70°，则∠FEC =（ ）

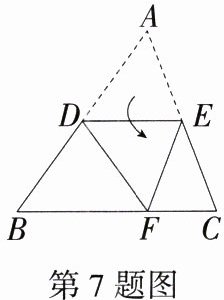
A.50°
B.40°
C.30°
D.20°

答案： B
∵ DE // BC，∠C = 70°，
∴ ∠AED = ∠C = 70°，由折叠得 ∠DEF = ∠AED = 70°，
∴ ∠FEC = 180° - ∠AED - ∠DEF = 180° - 70° - 70° = 40°，故选 B.

8.（2024 山东德州五中月考）长方形纸带中∠DEF = 25°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE的度数是（ ）


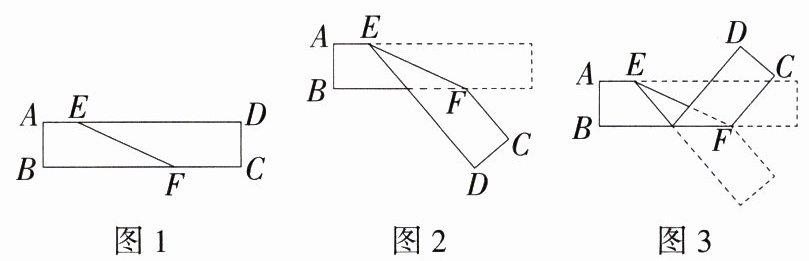
A.105°
B.120°
C.130°
D.145°

答案： A
∵ 四边形 ABCD 为长方形，
∴ AD // BC，
∴ ∠BFE = ∠DEF = 25°. 由翻折的性质可知题图 2 中，∠EFC = 180° - ∠BFE = 155°，
∴ ∠BFC = ∠EFC - ∠BFE = 130°，
∴ 题图 3 中，∠CFE = ∠BFC - ∠BFE = 105°. 故选 A.

9.（一题多解）（2023 广东深圳宝安一模）小刚利用如图（1）（2）（3）（4）所示的方法可以折出“过已知直线外一点和已知直线平行”的直线，现由实物抽象出数学图形则可得AD//BC，如图（5），过已知点A作线段AB交BC于点B，∠BAC = 35°，则∠ABC的度数为（ ）


A.50°
B.55°
C.60°
D.65°

答案： B 【解法一】由题意得 ∠CAD = 90°，
∴ ∠BAD = ∠CAD + ∠BAC = 125°，
∵ AD // BC，
∴ ∠ABC = 180° - ∠BAD = 55°. 【解法二】
∵ ∠ACB = 90°，∠BAC = 35°，
∴ ∠ABC = 180° - ∠ACB - ∠BAC = 180° - 90° - 35° = 55°. 故选 B.