第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
14.情境题·数学文化(2023江苏盐城中考)我国古代数学著作《九章算术》中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:“几个人一起去购买某物品,每人出8钱,则多出3钱;每人出7钱,则还差4钱.问人数、物品的价格分别是多少?”该问题中的人数为________.
答案:
7
解析:设该问题中的人数为 x,物品的价格为 y 钱,根据题意得$\begin{cases}8x - y = 3\\y - 7x = 4\end{cases}$,解得$\begin{cases}x = 7\\y = 53\end{cases}$,
∴ 该问题中的人数为 7.
解析:设该问题中的人数为 x,物品的价格为 y 钱,根据题意得$\begin{cases}8x - y = 3\\y - 7x = 4\end{cases}$,解得$\begin{cases}x = 7\\y = 53\end{cases}$,
∴ 该问题中的人数为 7.
15.跨物理·光的反射(2024河南郑州经开区外国语学校模拟)汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,在井口放置一面平面镜可改变光路,如图,当太阳光线AB与地面CD所成夹角∠ABC = 50°时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需使平面镜EF与地面的夹角∠EBC = ________.
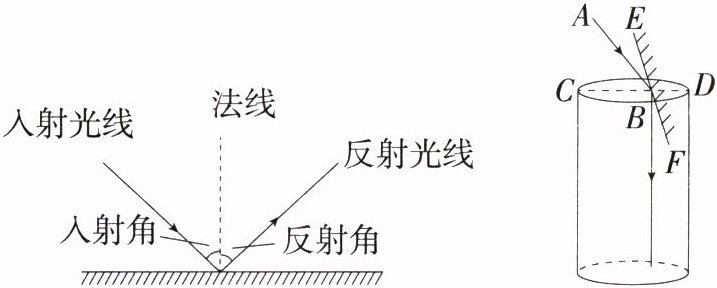

答案:
70°\n**解析**:如图,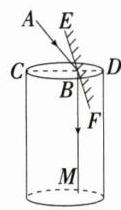
∵ BM⊥CD,
∴ ∠CBM = 90°,
∵ ∠ABC = 50°,
∴ ∠ABE + ∠FBM = 180° - 90° - 50° = 40°,
∵ ∠ABE = ∠FBM,
∴ ∠ABE = ∠FBM = 20°,
∴ ∠EBC = 20° + 50° = 70°.
70°\n**解析**:如图,

∵ BM⊥CD,
∴ ∠CBM = 90°,
∵ ∠ABC = 50°,
∴ ∠ABE + ∠FBM = 180° - 90° - 50° = 40°,
∵ ∠ABE = ∠FBM,
∴ ∠ABE = ∠FBM = 20°,
∴ ∠EBC = 20° + 50° = 70°.
16.(2024江苏盐城期中)如图,已知直线AB,CD被直线AC所截,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE = α,∠DCE = β.下列各式:①α+β;②α-β;③β-α;④180°-α-β;⑤360°-α-β.其中可以作为∠AEC的度数的是________.(填序号)
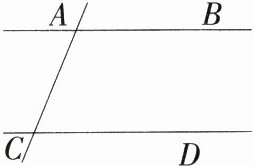

答案:
①②③⑤
解析:分情况讨论:(1)如图 1,由 AB//CD,可得∠AOC = ∠DCE = β,
∴ ∠AOE = 180° - ∠AOC = 180° - β,
∴ ∠AEC = 180° - α - (180° - β) = β - α.
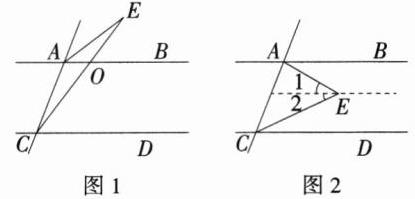
(2)如图 2,过 E 作 AB 的平行线,由 AB//CD,可得∠1 = ∠BAE = α,∠2 = ∠DCE = β,
∴ ∠AEC = α + β.
(3)如图 3,由 AB//CD,可得∠BOE = ∠DCE = β,
∵ ∠BAE = α,
∴ ∠OAE = 180° - α,
∴ ∠AEC = 180° - ∠BOE - ∠OAE = 180° - β - (180° - α) = α - β.
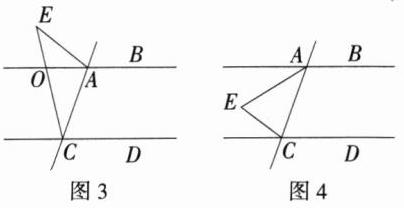
(4)如图 4,由 AB//CD 可得∠BAE + ∠AEC + ∠DCE = 360°,
∴ ∠AEC = 360° - α - β.
(5)当点 E 在 CD 的下方时,同(1)(3)可得∠AEC = α - β 或∠AEC = β - α.
综上所述,∠AEC 的度数可能为 β - α,α + β,α - β,360° - α - β,可以表示∠AEC 的度数的有①②③⑤,故答案为①②③⑤.
①②③⑤
解析:分情况讨论:(1)如图 1,由 AB//CD,可得∠AOC = ∠DCE = β,
∴ ∠AOE = 180° - ∠AOC = 180° - β,
∴ ∠AEC = 180° - α - (180° - β) = β - α.

(2)如图 2,过 E 作 AB 的平行线,由 AB//CD,可得∠1 = ∠BAE = α,∠2 = ∠DCE = β,
∴ ∠AEC = α + β.
(3)如图 3,由 AB//CD,可得∠BOE = ∠DCE = β,
∵ ∠BAE = α,
∴ ∠OAE = 180° - α,
∴ ∠AEC = 180° - ∠BOE - ∠OAE = 180° - β - (180° - α) = α - β.

(4)如图 4,由 AB//CD 可得∠BAE + ∠AEC + ∠DCE = 360°,
∴ ∠AEC = 360° - α - β.
(5)当点 E 在 CD 的下方时,同(1)(3)可得∠AEC = α - β 或∠AEC = β - α.
综上所述,∠AEC 的度数可能为 β - α,α + β,α - β,360° - α - β,可以表示∠AEC 的度数的有①②③⑤,故答案为①②③⑤.
17.[答案含评分细则](12分)解方程组:
(1)$\begin{cases}2x + y = 7 \\ 2x - 3y = 3\end{cases}$
(2)$\begin{cases}\frac{x + 1}{3} + \frac{y}{2} = 1 \\ \frac{x}{2} - \frac{1}{4}y - 2 = 0\end{cases}$
(3)$\begin{cases}2x - 3y + 4z = 12 \\ x - y + 3z = 4 \\ 4x + y - 3z = -2\end{cases}$
(1)$\begin{cases}2x + y = 7 \\ 2x - 3y = 3\end{cases}$
(2)$\begin{cases}\frac{x + 1}{3} + \frac{y}{2} = 1 \\ \frac{x}{2} - \frac{1}{4}y - 2 = 0\end{cases}$
(3)$\begin{cases}2x - 3y + 4z = 12 \\ x - y + 3z = 4 \\ 4x + y - 3z = -2\end{cases}$
答案:
解析:\n(1)$\begin{cases}2x + y = 7①\\2x - 3y = 3②\end{cases}$,① - ②得 4y = 4,解得 y = 1,将 y = 1 代入①,解得 x = 3,则方程组的解为$\begin{cases}x = 3\\y = 1\end{cases}$.\n(2)整理方程组得$\begin{cases}2x + 3y = 4①\\2x - y = 8②\end{cases}$,① - ②得 4y = - 4,解得 y = - 1,把 y = - 1 代入②得 2x + 1 = 8,解得 x = $\frac{7}{2}$,则原方程组的解为$\begin{cases}x = \frac{7}{2}\\y = - 1\end{cases}$.\n(3)$\begin{cases}2x - 3y + 4z = 12①\\x - y + 3z = 4②\\4x + y - 3z = - 2③\end{cases}$,① + ③×3,得 14x - 5z = 6④,② + ③,得 5x = 2,解得 x = $\frac{2}{5}$,把 x = $\frac{2}{5}$代入④,得$\frac{28}{5}$ - 5z = 6,解得 z = - $\frac{2}{25}$,把 x = $\frac{2}{5}$,z = - $\frac{2}{25}$代入②,得$\frac{2}{5}$ - y - $\frac{6}{25}$ = 4,解得 y = - $\frac{96}{25}$,则原方程组的解为$\begin{cases}x = \frac{2}{5}\\y = - \frac{96}{25}\\z = - \frac{2}{25}\end{cases}$.
18.[答案含评分细则](2023江苏扬州梅岭中学期中)(8分)已知关于x,y的方程组$\begin{cases}ax + 7y = 15① \\ 4x - by = -2②\end{cases}$,由于甲看错了方程①中的a,得到方程组的解为$\begin{cases}x = -2 \\ y = 1\end{cases}$,乙看错了方程②中的b,得到方程组的解为$\begin{cases}x = 4 \\ y = 1\end{cases}$,求$b^a$的值.
答案:
解析:把$\begin{cases}x = - 2\\y = 1\end{cases}$代入②,得 - 8 - b = - 2,解得 b = - 6,把$\begin{cases}x = 4\\y = 1\end{cases}$代入①,得 4a + 7 = 15,解得 a = 2,所以$b^a = (- 6)^2 = 36$.
查看更多完整答案,请扫码查看


