《2025年5年中考3年模拟七年级数学下册青岛版》

10.（2022青海中考,6,★☆☆）数学课上老师用双手形象地表示了“三线八角”图形，如图所示（两大拇指代表被截直线，食指代表截线）.从左至右依次表示(M7208003) ( )

A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角

答案： D：根据同位角、内错角、同旁内角的概念，可知题目中第一个图表示同位角，第二个图表示内错角，第三个图表示同旁内角，故选 D.

11.山东潍坊题型·多选题（2024山东潍坊潍城期中,9,★☆☆）如图，下列说法正确的是(M7208003) ( )
A.∠1与∠2是对顶角
B.∠1与∠4是内错角
C.∠1与∠B是同位角
D.∠4与∠D是同旁内角

答案： AD：A. ∠1 与∠2 是对顶角；B. ∠1 与∠4 不是内错角；C. ∠1 与∠B 不是同位角；D. ∠4 与∠D 是同旁内角. 故选 AD.

12.（2023山东德州齐河期中,6,★☆☆）如图，已知a//b，则图中内错角的对数是(M7208003) ( )

A.4
B.8
C.12
D.16

答案：
D：如图所示：
 内错角有∠1 与∠4，∠1 与∠5，∠7 与∠13，∠12 与∠4，∠6 与∠7，∠6 与∠8，∠16 与∠2，∠16 与∠9，∠15 与∠8，∠12 与∠3，∠14 与∠5，∠13 与∠17，∠11 与∠8，∠10 与∠5，∠16 与∠17，∠16 与∠3，共有 16 对. 故选 D.

13.（2023山东济宁微山期中,15,★☆☆）如图，在∠1，∠2，∠3，∠4，∠5和∠C中，同位角对数为a，内错角对数为b，同旁内角对数为c，则abc = _______.(M7208003)

答案： 答案：16 解析：同位角有∠1 与∠C，∠5 与∠C，共 2 对；内错角有∠2 与∠4，∠3 与∠5，共 2 对；同旁内角有∠2 与∠5，∠3 与∠4，∠4 与∠C，∠3 与∠C，共 4 对.
∴a = 2，b = 2，c = 4，
∴abc = 2×2×4 = 16，故答案为 16.

14.（2024山东德州五中学月考,16,★☆☆）如图，有下列说法：①能与∠DEF构成内错角的角有2个；②能与∠BFE构成同位角的角有2个；③能与∠C构成同旁内角的角有4个.其中正确结论的序号是________.(M7208003)

答案： 答案：① 解析：①能与∠DEF 构成内错角的角有 2 个，即∠EFA 和∠EDC，故正确；②能与∠BFE 构成同位角的角只有 1 个，即∠FAE，故错误；③能与∠C 构成同旁内角的角有 5 个，即∠CDE，∠B，∠CED，∠CEF，∠A，故错误. 所以结论正确的是①.

15.（2024甘肃陇南成县月考,22,★☆☆）如图，BF，DE相交于点A，BG交BF于点B，交AC于点C.(M7208003)
(1)指出DE，BC被BF所截形成的同位角、内错角、同旁内角.
(2)指出DE，BC被AC所截形成的内错角.
(3)指出FB，BC被AC所截形成的同旁内角.

答案： 解析：
(1) 同位角：∠FAE 和∠B；内错角：∠B 和∠DAB；同旁内角：∠EAB 和∠B.
(2) ∠EAC 和∠BCA，∠DAC 和∠ACG 都是内错角.
(3) ∠BAC 和∠BCA，∠FAC 和∠ACG 都是同旁内角.

16.抽象能力 复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零是一种常见的数学解题思想.
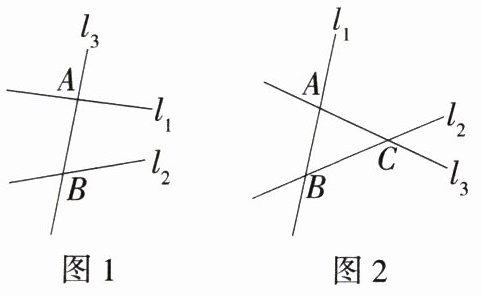
(1)如图1，直线l1，l2被直线l3所截，在这个基本图形中，形成了_______对同旁内角.
(2)如图2，平面内三条直线l1，l2，l3两两相交，交点分别为A、B、C，图中一共有_______对同旁内角.
(3)平面内四条直线两两相交，最多可以形成_______对同旁内角.
(4)平面内n条直线两两相交，最多可以形成_______对同旁内角.

答案： 答案：
(1)2
(2)6
(3)24
(4)n(n - 1)(n - 2) 解析：
(1) 直线 l₁，l₂ 被直线 l₃ 所截，在这个基本图形中，形成了 2 对同旁内角.
(2) 平面内三条直线 l₁，l₂，l₃ 两两相交，交点分别为 A、B、C，题图中一共有 6 = 3×2×1 对同旁内角.
(3) 平面内四条直线两两相交，交点最多有 6 个，如图，可知任意不同的两条直线都可被另外的两条直线所截，所以任意不相同的两条直线可以形成 4 对同旁内角，4 条直线共有 6 种两条直线被另两条直线所截的情况，所以有 4×(4 - 1)×(4 - 2)= 24 对同旁内角.
(4) 平面内 n 条直线两两相交，最多可以形成 n(n - 1)(n - 2)对同旁内角.