《2025年5年中考3年模拟七年级数学下册青岛版》

10.(2024山东枣庄峄城东方国际学校月考,4,★☆☆)已知$7^{x}=y$,则$7^{x + 1}=$（ ）
A.x
B.1 + y
C.7 + y
D.7y

答案： D
∵$7^{x}$ = y,
∴$7^{x + 1}$ = $7^{x}$·7 = 7y. 故选 D.

11.(2022山东济南十二月考,6,★☆☆)已知$2^{a}=5$,$2^{b}=10$,$2^{c}=50$,那么a,b,c之间满足的等量关系是(M7210001)（ ）
A.$ab = c$
B.$a + b = c$
C.$a:b:c = 1:2:10$
D.$a^{2}b^{2}=c^{2}$

答案： B
∵ 5×10 = 50,$2^{a}$ = 5,$2^{b}$ = 10,$2^{c}$ = 50,
∴$2^{a}$·$2^{b}$ = $2^{c}$,
∴$2^{a + b}$ = $2^{c}$,
∴ a + b = c, 故选 B.

12.(2024山东聊城冠县期中,15,★☆☆)已知$x\cdot x^{m}\cdot x^{n}=x^{14}(x\neq1)$,且m比n大3,则mn的值为_________.(M7210001)

答案： 答案 40 解析
∵ x·$x^{m}$·$x^{n}$ = $x^{1 + m + n}$ = $x^{14}$,
∴ 1 + m + n = 14, 即 m + n = 13①,
∵ m 比 n 大 3,
∴ m - n = 3②, 联立①②得 $\begin{cases}m + n = 13\\m - n = 3\end{cases}$, 解得 $\begin{cases}m = 8\\n = 5\end{cases}$,
∴ mn = 8×5 = 40.

13.新考向·新定义试题(2024山东日照东港新营中学月考,14,★☆☆)对数的定义:一般地,若$a^{x}=N(a ＞ 0,a\neq1)$,那么x叫作以a为底N的对数,记作$x = \log_{a}N$.比如指数式$2^{4}=16$可以转化为$4 = \log_{2}16$,对数式$2 = \log_{5}25$可以转化为$5^{2}=25$.我们根据对数的定义可得到对数的一个性质:$\log_{a}(M\cdot N)=\log_{a}M+\log_{a}N(a ＞ 0,a\neq1,M ＞ 0,N ＞ 0)$.理由如下:设$\log_{a}M = m$,$\log_{a}N = n$,则$M = a^{m}$,$N = a^{n}$,$\therefore M\cdot N = a^{m}\cdot a^{n}=a^{m + n}$,由对数的定义得$m + n = \log_{a}(M\cdot N)$,又$\because m + n = \log_{a}M+\log_{a}N$,$\therefore \log_{a}(M\cdot N)=\log_{a}M+\log_{a}N$,同理还可以证明对数的另一个性质:$\log_{a}\frac{M}{N}=\log_{a}M-\log_{a}N(a ＞ 0,a\neq1,M ＞ 0,N ＞ 0)$.请利用以上信息计算:$\log_{3}54+\log_{3}2-\log_{3}4=$_________.

答案： 答案 3 解析 $log_{3}54 + log_{3}2 - log_{3}4$ = $log_{3}(54×2÷4)$ = $log_{3}27$ = $log_{3}3^{3}$ = 3.

14.(2024山东菏泽牡丹月考,15,★☆☆)计算:
(1)$(-m)\cdot (-m)^{2}\cdot (-m)^{3}$.
(2)$(m - n)\cdot (n - m)^{3}\cdot (n - m)^{4}$.

答案： 解析
(1) (-m)·(-m)$^{2}$·(-m)$^{3}$ = (-m)$^{1 + 2 + 3}$ = (-m)$^{6}$ = $m^{6}$.
(2) (m - n)·(n - m)$^{3}$·(n - m)$^{4}$ = (m - n)·[-(m - n)$^{3}$]·(m - n)$^{4}$ = -(m - n)$^{8}$.

15.新考向·新定义试题(2024山东济南章丘一中期中,21,★☆☆)规定新运算“*”:$a*b = 2^{a}\times2^{b}$,如:$1*3 = 2^{1}\times2^{3}=2^{4}=16$.
(1)求$3*5$的值.
(2)若$2*(2x + 1)=64$,求x的值.

答案： 解析
(1) 由题意可得 3 * 5 = $2^{3}$×$2^{5}$ = $2^{8}$ = 256.
(2) 由题意可得 2 * (2x + 1) = $2^{2}$·$2^{2x + 1}$ = $2^{2x + 3}$. 因为 2 * (2x + 1) = 64 = $2^{6}$, 所以 2x + 3 = 6, 解得 x = $\frac{3}{2}$.

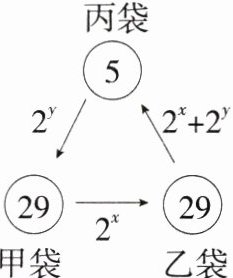
16.运算能力(2024山东淄博博山一模)如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出$2^{x}$个球放入乙袋,再从乙袋中取出$(2^{x}+2^{y})$个球放入丙袋,最后从丙袋中取出$2^{y}$个球放入甲袋,此时三只袋中球的个数相同,则$2^{x + y}$的值为（ ）

A.128
B.64
C.32
D.16

答案： A 由题意, 得 5 - $2^{y}$ + $2^{x}$ + $2^{y}$ = 29 + $2^{y}$ - $2^{x}$ = 29 + $2^{x}$ - $2^{x}$ - $2^{y}$, 即 5 + $2^{x}$ = 29 + $2^{y}$ - $2^{x}$ = 29 - $2^{y}$,
∴ $\begin{cases}2·2^{x} - 2^{y} = 24\\2·2^{y} = 2^{x}\end{cases}$, 解得 $\begin{cases}2^{x} = 16\\2^{y} = 8\end{cases}$,
∴$2^{x + y}$ = $2^{x}$·$2^{y}$ = 16×8 = 128, 故选 A.