《2025年5年中考3年模拟七年级数学下册青岛版》

1.(2024辽宁中考)下列计算正确的是(M7210002) ( )
A.$a^{2}+a^{3}=2a^{5}$
B.$a^{2}\cdot a^{3}=a^{6}$
C.$(a^{2})^{3}=a^{5}$
D.$a(a + 1)=a^{2}+a$

答案： D：$a^{2}$与$a^{3}$不是同类项，不能合并；$B$选项$a^{2}\cdot a^{3}=a^{5}\neq a^{6}$；$C$选项$(a^{2})^{3}=a^{6}\neq a^{5}$；$D$选项$a(a + 1)=a^{2}+a$，故选 D。

2.(2024广东深圳龙华红山中学月考)计算$-2a(a^{2}-1)$的结果是(M7210002) ( )
A.$-2a^{3}+2a$
B.$-2a^{3}+a$
C.$-2a^{3}-2a$
D.$-a^{3}+2a$

答案： A：$-2a(a^{2}-1)=-2a\cdot a^{2}+2a\cdot1=-2a^{3}+2a$，故选 A。

3.数形结合思想(2024河北承德兴隆期中)如图,将一边长为m的三个长方形拼在一起,用不同的方法表示整个图形的面积可以说明下列哪个等式成立(M7210002) ( )

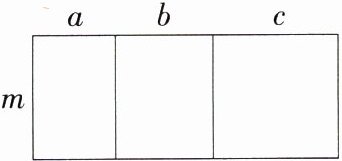
A.$m(a + b + c)=ma+mb+mc$
B.$(a + b)m=ma+mb$
C.$a(a + b + c)=a^{2}+ab+ac$
D.$(b + c)m=bm+cm$

答案： A：由题意可得$m(a + b + c)=ma+mb+mc$，故选 A。

4.(2024山东泰安肥城月考)下列计算错误的是(M7210002) ( )
A.$-4a(2a^{2}+3a - 1)=-8a^{3}-12a^{2}+4a$
B.$a^{m}(a^{m}-a^{2}+1)=a^{mm}-a^{2m}+a^{m}$
C.$(-3x^{2})\cdot(4x^{2}-\frac{4}{9}x + 1)=-12x^{4}+\frac{4}{3}x^{3}-3x^{2}$
D.$(2a^{2}-\frac{2}{3}a-\frac{4}{9})\cdot(-9a)=-18a^{3}+6a^{2}+4a$

答案： B：$A$选项$-4a(2a^{2}+3a - 1)=-8a^{3}-12a^{2}+4a$；$B$选项$a^{m}(a^{m}-a^{2}+1)=a^{2m}-a^{m + 2}+a^{m}$；$C$选项$(-3x^{2})\cdot(4x^{2}-\frac{4}{9}x + 1)=-12x^{4}+\frac{4}{3}x^{3}-3x^{2}$；$D$选项$(2a^{2}-\frac{2}{3}a-\frac{4}{9})\cdot(-9a)=-18a^{3}+6a^{2}+4a$。 故选 B。

5.(2024广东深圳福田期末)计算:$2x(x - 1)=$______. (M7210002)

答案： 答案：$2x^{2}-2x$ 解析：$2x(x - 1)=2x^{2}-2x$。

6.(2024山东淄博张店八中月考)若三角形的一边长为$2m + 1$,这条边上的高为$2m$,则此三角形的面积为______. (M7210002)

答案： 答案：$2m^{2}+m$ 解析：由题意得，此三角形的面积$\frac{1}{2}\times(2m + 1)\times2m=2m^{2}+m$。

7.新独家原创 已知$(a + b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$,则$(2m - 1)^{3}(-2mn)$的值为______. (M7210002)

答案： 答案：$-16m^{4}n+24m^{3}n-12m^{2}n+2mn$ 解析：$(2m - 1)^{3}(-2mn)=(8m^{3}-12m^{2}+6m - 1)\cdot(-2mn)=-16m^{4}n+24m^{3}n-12m^{2}n+2mn$。

8.计算:(M7210002)
(1)$-2x^{3}y\cdot(3xy^{2}-3xy + 1)$.
(2)$xy(-x^{2}y+xy^{5}-x^{3}y^{2})$.

答案： 解析：
(1)$-2x^{3}y\cdot(3xy^{2}-3xy + 1)=-2x^{3}y\cdot3xy^{2}-(-2x^{3}y)\cdot3xy+(-2x^{3}y)\times1=-6x^{4}y^{3}+6x^{4}y^{2}-2x^{3}y$。
(2)$xy(-x^{2}y+xy^{5}-x^{3}y^{2})=xy\cdot(-x^{2}y)+xy\cdot xy^{5}-xy\cdot x^{3}y^{2}=-x^{3}y^{2}+x^{2}y^{6}-x^{4}y^{3}$。

9.教材变式 解方程:(M7210002)
$x(3x - 4)+2x(x + 7)=5x(x - 7)+90$.

答案： 解析：去括号，得$3x^{2}-4x+2x^{2}+14x=5x^{2}-35x+90$，移项，得$3x^{2}-4x+2x^{2}+14x-5x^{2}+35x=90$，合并同类项，得$45x=90$，系数化为 1，得$x = 2$。

10.(2024河北沧州孟村期末,9,★☆☆)要使$-x^{3}(x^{2}+ax + 1)+2x^{4}$中不含有x的四次项,则a等于 ( ) (M7210002)
A.1
B.2
C.3
D.4

答案： B：原式$=-x^{5}-ax^{4}-x^{3}+2x^{4}=-x^{5}+(2 - a)x^{4}-x^{3}$。 因为$-x^{3}(x^{2}+ax + 1)+2x^{4}$中不含有$x$的四次项，所以$2 - a = 0$，解得$a = 2$，故选 B。

11.(2024陕西咸阳市实验中学月考,7,★☆☆)已知$A=x^{2}+3x - a$,$B=-x$,$C=x^{3}+3x^{2}+5$,若$A\cdot B + C$的值与x的取值无关,当$x=-4$时,A的值为 ( ) (M7210002)
A.0
B.4
C.-4
D.2

答案： B：因为$A=x^{2}+3x - a$，$B=-x$，$C=x^{3}+3x^{2}+5$，所以$A\cdot B + C=(x^{2}+3x - a)(-x)+(x^{3}+3x^{2}+5)=-x^{3}-3x^{2}+ax+x^{3}+3x^{2}+5=ax + 5$。 因为$A\cdot B + C$的值与$x$的取值无关，所以$a = 0$，所以$A=x^{2}+3x$，当$x=-4$时，$A=(-4)^{2}+3\times(-4)=4$，故选 B。