《2025年5年中考3年模拟七年级数学下册青岛版》

8. (2024山东日照东港月考)两条平行线被第三条直线所截，则内错角的平分线的位置关系是 ( )
A. 互相垂直
B. 互相平行
C. 相交但不垂直
D. 平行或相交都有可能

答案：
B 如图，
∵ AD//BC，
∴ ∠DEF = ∠BFE，
∵ EM平分∠DEF，FN平分∠BFE，
∴ ∠1 = $\frac{1}{2}$∠DEF，∠2 = $\frac{1}{2}$∠BFE，
∴ ∠1 = ∠2，
∴ EM//FN， 即当两条平行线被第三条直线所截时，内错角的平分线互相平行，故选B。

9. 【等积法】(2024山东青岛市北月考)如图，$AC\perp BC$，垂足为$C$，$AC = 6$，$BC = 8$，$AB = 10$. $P$是线段$AB$上一点，连接$PC$，$PC$的长不可能是 ( )

A. $4$
B. $5$
C. $6$
D. $7$

答案：
A 如图，作CH⊥AB于H，
∵ AC⊥BC，
∴ △ABC的面积 = $\frac{1}{2}$AC·BC = $\frac{1}{2}$AB·CH，
∵ AC = 6，BC = 8，AB = 10，
∴ CH = 4.8，
∵ CH≤PC＜BC，即4.8≤PC＜8，
∴ PC的长不可能为4。故选A。

10. 【平行线拐点模型】(2022山东青岛市南期末)如图，一条公路修到湖边时，需拐弯绕道而过，若第一个拐角$\angle A$的度数为$\alpha$，第二个拐角$\angle B$的度数为$\beta$，第三个拐角是$\angle C$，这时的道路$CE$恰好与第一次拐弯之前的道路$AD$平行，则$\angle C$的度数为 ( )

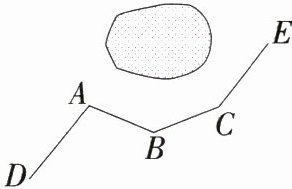
A. $\alpha - \beta$
B. $180^{\circ} - \beta + \alpha$
C. $360^{\circ} - \beta - \alpha$
D. $\beta - \alpha$

答案：
B 如图，过B作BF//AD，
∵ CE//AD，
∴ AD//BF//CE，
∴ ∠ABF = ∠A = α，∠FBC = 180° - ∠C，
∵ ∠ABC = ∠ABF + ∠FBC = β，
∴ α + 180° - ∠C = β，
∴ ∠C = 180° - β + α， 故选B。

11. 【易错题】(2023湖南永州中考)如图，$AB// CD$，$BC// ED$，$\angle B = 80^{\circ}$，则$\angle D =$________度.(M7208005)

答案： 答案 100 解析
∵ AB//CD，∠B = 80°，
∴ ∠BCD = ∠B = 80°，
∵ BC//ED，
∴ ∠D + ∠BCD = 180°，
∴ ∠D = 180° - ∠BCD = 180° - 80° = 100°。

12. 【平行线+角平分线模型】(2024福建龙岩长汀一模)如图，$AB// CD$，直线$EF$交$AB$于点$E$，交$CD$于点$F$，$EG$平分$\angle BEF$，交$CD$于点$G$，$\angle 1 = 50^{\circ}$，则$\angle 2$等于________.

答案： 答案 65° 解析
∵ AB//CD，
∴ ∠1 + ∠BEF = 180°，
∵ ∠1 = 50°，
∴ ∠BEF = 130°，
∵ EG平分∠BEF，
∴ ∠BEG = $\frac{1}{2}$∠BEF = 65°，
∴ ∠2 = ∠BEG = 65°。

13. (2022山东济南期中)如图，点$A$，$B$，$C$，$D$在同一条直线上，若满足条件________，则有$AE// BF$.(要求：不添加辅助线，填一个答案即可)

答案： 答案 ∠5 = ∠A（答案不唯一） 解析 添加∠5 = ∠A，可根据“同位角相等，两直线平行”判定AE//BF。（答案不唯一）

14. 【情境题·现实生活】(2024山东潍坊高密期中)某小地区地下停车场的限高栏杆的示意图如图所示，当栏杆抬起到最大高度时，$\angle ABC = 120^{\circ}$，若此时$CD$平行于地面$AE$，则$\angle BCD =$________度.

答案：
答案 150 解析 过点B作BF//CD，如图， 由题意可知∠ABF = 90°，
∵ ∠ABC = 120°，
∴ ∠FBC = ∠ABC - ∠ABF = 120° - 90° = 30°，
∵ BF//CD，
∴ ∠FBC + ∠BCD = 180°，
∴ ∠BCD = 180° - ∠FBC = 180° - 30° = 150°。故答案为150。

15. 【分类讨论思想】(2024山东菏泽牡丹月考)将一副直角三角尺的直角顶点按如图所示的方式叠放在一起(其中$\angle A = 60^{\circ}$，$\angle D = 30^{\circ}$，$\angle E = \angle B = 45^{\circ}$)，当$\angle ACE ＜ 180^{\circ}$，且点$E$在直线$AC$的上方时，满足三角尺$BCE$有一条边与三角尺$ACD$的斜边$AD$平行，那么此时$\angle ACE =$________________.

答案：
答案 30°或120°或165° 解析 分情况讨论：①如图1，当AD//CE时，∠DCE = ∠D = 30°，
∴ ∠ACE = 90° + 30° = 120°。 ②如图2，当AD//BE时，延长BC交AD于点M，则∠AMC = ∠B = 45°，∠MCE = 90°，
∴ ∠ACM = 180° - 45° - 60° = 75°，
∴ ∠ACE = ∠ACM + ∠MCE = 75° + 90° = 165°。 ③如图3，当AD//BC时，
∵ AD//BC，
∴ ∠D = ∠BCD = 30°，
∵ ∠ACE + ∠ECD = ∠ECD + ∠DCB = 90°，
∴ ∠ACE = ∠DCB = 30°。 故答案为30°或120°或165°。

16. (2024山东潍坊安丘期中)如图，已知射线$OP// AE$，$\angle A = \alpha$，依次作出$\angle AOP$的平分线$OB$，$\angle BOP$的平分线$OB_1$，$\angle B_1OP$的平分线$OB_2$，……，$\angle B_{n - 1}OP$的平分线$OB_n$，其中点$B$，$B_1$，$B_2$，…，$B_n$都在射线$AE$上，则$\angle AB_{2024}O =$________.

答案： 答案 $\frac{180° - \alpha}{2^{2025}}$ 解析
∵ OP//AE，∠A = α，
∴ ∠ABO = ∠POB = $\frac{1}{2}$(180° - α)，
∴ ∠AB₁O = $\frac{1}{2}$(180° - ∠OBB₁) = $\frac{1}{2}$∠ABO = $\frac{1}{4}$(180° - α)，同理∠AB₂O = $\frac{1}{8}$(180° - α)，……，则∠ABₙO = $\frac{180° - \alpha}{2^{n + 1}}$。
∴ ∠AB₂₀₂₄O = $\frac{180° - \alpha}{2^{2025}}$。 故答案为$\frac{180° - \alpha}{2^{2025}}$。