《2025年5年中考3年模拟七年级数学下册青岛版》

1.(2023贵州中考)如图,AB//CD,AC与BD相交于点E.若∠C = 40°,则∠A的度数是 ( )

A.39°
B.40°
C.41°
D.42°

答案： B 因为AB//CD，所以∠A = ∠C，又因为∠C = 40°，所以∠A = 40°，故选B。

2.(2023湖南岳阳中考)如图,已知AB//CD,点E在直线AB上,点F,G在直线CD上,EG⊥EF于点E,∠AEF = 40°,则∠EGF的度数是 ( )

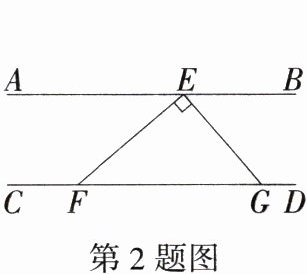
A.40°
B.45°
C.50°
D.60°

答案： C 因为EG⊥EF，所以∠FEG = 90°，因为∠AEF + ∠FEG + ∠BEG = 180°，∠AEF = 40°，所以∠BEG = 180° - ∠AEF - ∠FEG = 50°，又因为AB//CD，所以∠EGF = ∠BEG = 50°，故选C。

3.(2023辽宁丹东中考)如图所示,在△ABC中,CD⊥AB,垂足为点D,DE//AC,交BC于点E.若∠A = 50°,则∠CDE的度数是 ( )

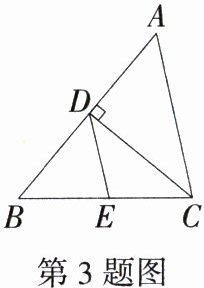
A.25°
B.40°
C.45°
D.50°

答案： B 因为DE//AC，∠A = 50°，所以∠BDE = ∠A = 50°，因为CD⊥AB，所以∠CDB = 90°，所以∠CDE = ∠CDB - ∠BDE = 90° - 50° = 40°，故选B。

4.(2023重庆中考A卷)如图,AB//CD,AD⊥AC,若∠1 = 55°,则∠2的度数为(M7208005) ( )

A.35°
B.45°
C.50°
D.55°

答案： A 因为AB//CD，所以∠BAC + ∠1 = 180°，因为∠1 = 55°，所以∠BAC = 125°，因为AD⊥AC，所以∠CAD = 90°，所以∠2 = ∠BAC - ∠CAD = 35°，故选A。

5.新独家原创 如图所示的是学校的伸缩门,已知各立柱均平行,现测得∠2 = 60°,则∠1 = ________.

答案：
答案 60° 解析 如图，因为各立柱均平行，∠1和∠2是同位角，所以∠1 = ∠2 = 60°。

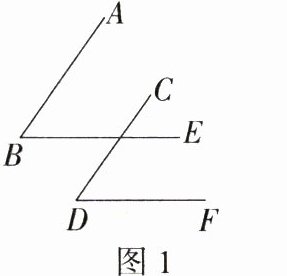
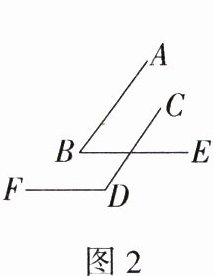
6.(2022山西晋中左权期中)为了落实“双减”政策,促进学生健康成长,各学校积极推行“5+2”模式,立足学生的认知成长规律,满足学生多样化的需求,打造特色突出、切实可行的体育锻炼内容.某学校将“抖空竹”引入阳光体育一小时活动,图1是一位同学抖空竹的一个瞬间,小丽把它抽象成图2,请解决以下数学问题:已知AB//CD,∠EAB = 80°,∠ECD = 110°,则∠E的度数是 ________.

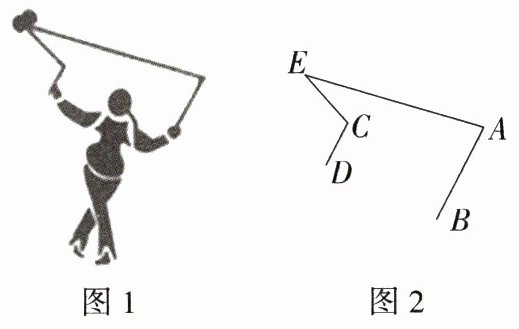
答案：
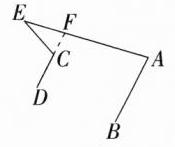
答案 30° 解析 如图，延长DC交AE于点F，因为AB//CD，所以∠EFC = ∠A = 80°，因为∠DCE = 110°，所以∠ECF = 70°，所以∠E = 180° - 70° - 80° = 30°。

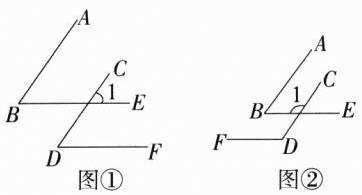
7.如图,∠B、∠D的两边分别平行.(M7208005)
(1)在图1中,∠B与∠D的关系为__________.
(2)在图2中,∠B与∠D的关系为__________.
(3)把(1)(2)中的结论用一句话归纳:______________________________.

答案：
答案 （1）相等 （2）互补 （3）如果两个角的两边分别平行，那么这两个角相等或互补 解析 （1）如图①，因为AB//CD，所以∠1 = ∠B，因为BE//DF，所以∠1 = ∠D，所以∠B = ∠D。 （2）如图②，因为AB//CD，所以∠B + ∠1 = 180°，因为BE//DF，所以∠D = ∠1，所以∠B + ∠D = 180°。 （3）把（1）（2）中的结论归纳得如果两个角的两边分别平行，那么这两个角相等或互补。

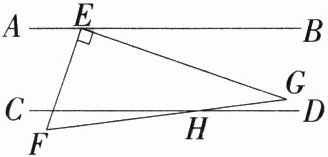
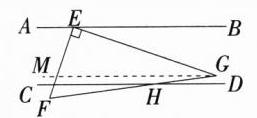
8.新独家原创 如图,AB//CD,点E在线段AB上,EG⊥EF,已知∠AEF = 70°,∠EGF = 30°,求∠GHD的度数.(M7208005)

答案：
解析 因为EG⊥EF，∠AEF = 70°，所以∠BEG = 180° - 90° - 70° = 20°。如图，过点G作GM//AB，则∠MGE = ∠BEG = 20°，因为∠EGF = 30°，所以∠FGM = 30° - 20° = 10°。因为AB//CD，MG//AB，所以MG//CD，所以∠GHD = ∠FGM = 10°。