《2025年5年中考3年模拟七年级数学下册青岛版》

9.(2024广东广州天河期末改编)某自行车的示意图如图所示，其中AB//CD，且都与地面l平行，若∠BAC = ∠ABC = 60°，则下列结论不正确的是 ( )

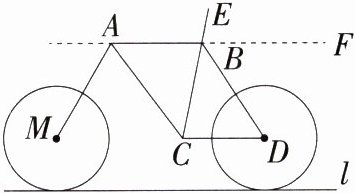
A.∠ACD = 120°
B.当∠MAC = 60°时，有AM//BC
C.当∠CBD = 30°时，有AC//BD
D.当∠DBF = 60°时，有AC//BD

答案： C：
∵ AB//CD，∠BAC = 60°，
∴ ∠ACD = 120°，故 A 选项结论正确，不符合题意；当∠MAC = 60°时，
∵ ∠BAC = 60°，
∴ ∠MAB = ∠MAC + ∠CAB = 120°，又
∵ ∠ABC = 60°，
∴ ∠MAB + ∠ABC = 180°，
∴ AM//BC，故 B 选项结论正确，不符合题意；当∠CBD = 30°时，∠ABD = ∠ABC + ∠CBD = 60° + 30° = 90°，
∴ ∠BAC + ∠ABD = 60° + 90° = 150°≠180°，
∴ AC 与 BD 不平行，故 C 选项结论错误，符合题意；当∠DBF = 60°时，∠CAB = ∠DBF = 60°，
∴ AC//BD，故 D 选项结论正确，不符合题意. 故选 C.

10.(2024山东潍坊高密期中改编)如图，AB//CD，P为AB上方一点，H，G分别为AB，CD上的点，∠PHB，∠PGD的平分线交于点E，∠PGC的平分线与EH的延长线交于点F，下列结论不正确的是 ( )

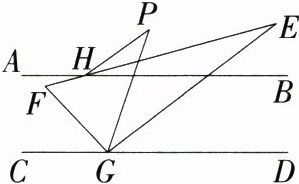
A.EG⊥FG
B.∠P = 2∠E
C.HP//GE
D.∠EHP + ∠FGP = ∠F

答案：
C：
∵ GF 平分∠PGC，GE 平分∠PGD，
∴ ∠PGF = $\frac{1}{2}$∠PGC，∠PGE = $\frac{1}{2}$∠PGD，
∴ ∠EGF = ∠PGF + ∠PGE = $\frac{1}{2}$(∠PGC + ∠PGD) = $\frac{1}{2}$×180° = 90°，
∴ EG⊥FG，故 A 结论正确，不符合题意；\n如图，设 PG 与 AB 交于 M，GE 与 AB 交于 N，过点 P 作 PQ//AB，过点 E 作 EK//AB，
则∠QPH = ∠PHB，∠KEH = ∠EHB，
∵ AB//CD，
∴ PQ//CD，EK//CD，
∴ ∠QPG = ∠PGD，∠KEG = ∠EGD，
∵ ∠QPG = ∠QPH + ∠HPG，
∴ ∠QPH + ∠HPG = ∠PGD，
∵ HE 平分∠PHB，GE 平分∠PGD，
∴ ∠PHB = 2∠EHB，∠PGD = 2∠EGD，
∴ ∠QPH = 2∠EHB，∠QPG = 2∠EGD，
∴ 2∠EHB + ∠HPG = 2∠EGD，
∴ ∠HPG = 2(∠EGD - ∠EHB)，
∵ ∠EGD - ∠EHB = ∠KEG - ∠KEH = ∠HEG，
∴ ∠HPG = 2∠HEG，故 B 结论正确，不符合题意；由已知条件不能证明 HP//GE，故 C 结论不正确，符合题意；\n如图，过点 F 作 FL//AB，
则 FL//AB//CD，
∴ ∠HFL = ∠EHB，∠LFG = ∠FGC，
∵ HE 平分∠PHB，GF 平分∠PGC，
∴ ∠EHB = ∠EHP，∠FGC = ∠FGP，
∴ ∠EHP + ∠FGP = ∠HFL + ∠LFG = ∠EFG，故 D 结论正确，不符合题意. 故选 C.

11.(2023山东聊城冠县期中)为了测量古塔的外墙底角(∠AOB)的度数，王明设计了如下方案：作AO、BO的延长线OD、OC，量出∠COD的度数，就得到了∠AOB的度数，王明这样做的依据是________________.

答案： 对顶角相等

12.如图，直线AB，CD相交于点O，OE⊥OF，OC平分∠AOE，且∠BOF = 2∠BOE，则∠BOD = ________.

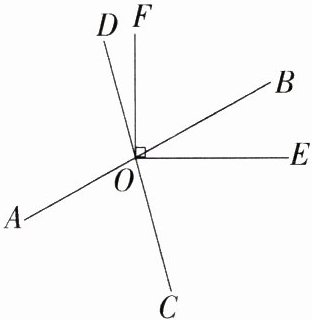
答案： 75°
解析：因为 OE⊥OF，所以∠EOF = 90°，因为∠BOF = 2∠BOE，所以 3∠BOE = 90°，所以∠BOE = 30°，所以∠AOE = 180° - ∠BOE = 180° - 30° = 150°. 因为 OC 平分∠AOE，所以∠AOC = $\frac{1}{2}$∠AOE = $\frac{1}{2}$×150° = 75°. 因为∠BOD 和∠AOC 是对顶角，所以∠BOD = ∠AOC = 75°.

13.(2024山东青岛市北期末)如图a，已知长方形纸带ABCD，将纸带沿EF折叠后，点C、D分别落在H、G的位置，再沿BC折叠，如图b所示，若∠DEF = 72°，则∠GMN = ________°.

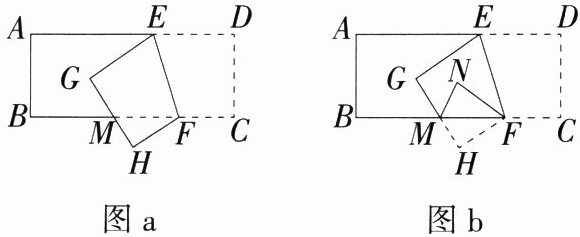
答案： 72解析：
∵ AD//CB，
∴ ∠EFC + ∠DEF = 180°，∠EFB = ∠DEF，
∵ ∠DEF = 72°，
∴ ∠EFH = ∠EFC = 180° - 72° = 108°，∠EFB = 72°，
∴ ∠BFH = 108° - 72° = 36°.
∵ ∠H = ∠C = 90°，
∴ ∠HMF = 180° - 90° - 36° = 54°. 由折叠可得∠NMF = ∠HMF = 54°，
∴ ∠GMN = 180° - ∠NMF - ∠HMF = 72°.