《2025年5年中考3年模拟七年级数学下册青岛版》

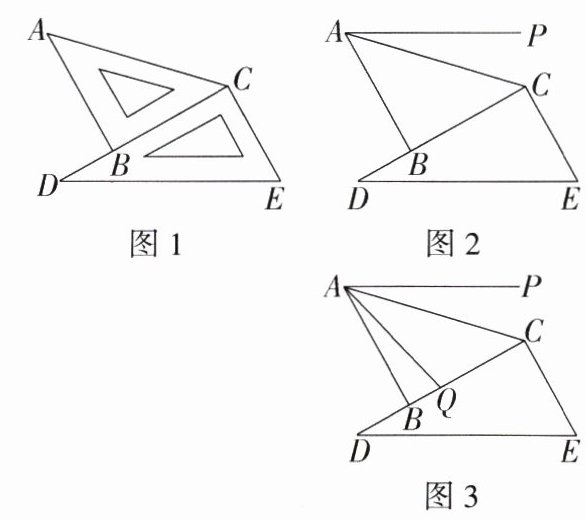
22.[答案含评分细则](2022湖北武汉青山期末)(12分)小聪把一副三角尺按如图1所示的方式摆放，其中边BC，DC在同一条直线上，过点A向右作射线AP，且AP//DE.
(1)如图2，求∠PAC的度数.
(2)如图3，点Q是线段BC上一点，若∠AQB = $\frac{5}{3}$∠PAQ，求∠QAB的度数.

答案：
解析：（1）过点 B 作 BF//DE，如图.
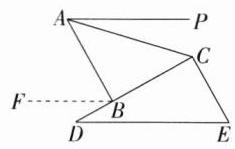
∵ BF//DE，
∴ ∠FBD = ∠D.
∵ AP//DE，
∴ AP//BF，
∴ ∠PAB = ∠ABF，
∴ ∠PAB + ∠D = ∠ABF + ∠FBD = ∠ABD，
∵ ∠D = 30°，∠ABD = 90°，
∴ ∠PAB = 60°.
∵ ∠BAC = 45°，
∴ ∠PAC = 15°.（2）同（1）易得∠PAQ + ∠D = ∠AQB，设∠PAQ = x，则∠AQB = $\frac{5}{3}$∠PAQ = $\frac{5}{3}x$，
∴ x + 30° = $\frac{5}{3}x$，解得 x = 45°，
∴ ∠AQB = 75°，
∴ ∠QAB = 180° - 90° - 75° = 15°.

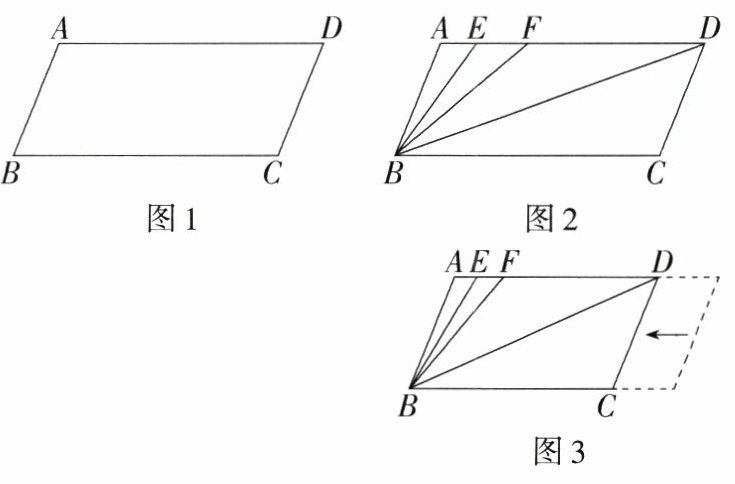
23.[答案含评分细则](2022重庆潼南期中)(14分)已知AD//BC，∠BAD = ∠BCD = 112°.
(1)如图1，易得∠B的度数为________，AB与DC的位置关系为________.
(2)如图2，若点E、F在AD上，且满足∠FBD = ∠CBD，BE平分∠ABF，则∠EBD的度数为________.
(3)在(2)的条件下，若平行移动DC到如图3所示的位置.
①在DC移动的过程中，∠BDA与∠BFA的度数的比值是否发生改变？若不改变，请求出其比值；若改变，请说明理由.
②当∠AEB = ∠BDC时，求∠BDC的度数.

答案： 解析：（1）68°；平行. 详解：
∵ AD//BC，
∴ ∠A + ∠B = 180°，∠D + ∠C = 180°，
∵ ∠A = ∠C = 112°，
∴ ∠B = ∠D = 68°，
∴ ∠B + ∠C = 180°，
∴ AB//CD.（2）34°. 详解：由（1）知∠ABC = 68°，
∵ BE 平分∠ABF，
∴ ∠ABE = ∠EBF，
∵ ∠FBD = ∠CBD，
∴ ∠EBD = $\frac{1}{2}$∠ABF + $\frac{1}{2}$∠CBF = $\frac{1}{2}$∠ABC = 34°.（3）①∠BDA 与∠BFA 的度数的比值不变.
∵ AD//BC，
∴ ∠ADB = ∠CBD，
∵ ∠FBD = ∠CBD，
∴ ∠FDB = ∠FBD，
∵ ∠AFB = 180° - ∠BFD = 180° - (180° - ∠FBD - ∠FDB) = ∠FBD + ∠FDB，
∴ ∠AFB = 2∠BDA，
∴ ∠BDA : ∠BFA = 1 : 2 = $\frac{1}{2}$.②设∠ABE = ∠EBF = α，∠FBD = ∠DBC = ∠FDB = β，
∵ AB//CD，
∴ ∠BDC = ∠ABD = 2α + β，
∵ ∠AEB = 180° - ∠BED = 180° - (180° - ∠EBD - ∠EDB) = ∠EBD + ∠EDB = α + 2β，∠AEB = ∠BDC，
∴ 2α + β = α + 2β，
∴ α = β，
∵ 2α + 2β = 68°，
∴ α = β = 17°，
∴ ∠BDC = 3α = 51°.