《2025年5年中考3年模拟七年级数学下册青岛版》

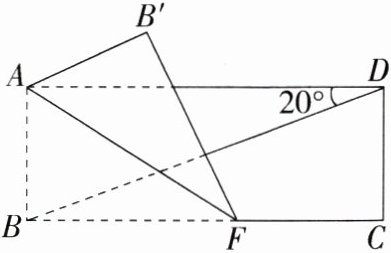
21. (10分)如图，把一张长方形纸条$ABCD$沿$AF$折叠，已知$\angle ADB = 20^{\circ}$，那么$\angle BAF$为多少度，才能使$AB'// BD$？(M7208005)

答案： 解析 ∠BAF = 55°。理由如下： 因为四边形ABCD是长方形， 所以AD//BC，∠ABC = 90°， 因为∠ADB = 20°，所以∠DBC = ∠ADB = 20°， 所以∠ABD = 70°。 要使AB′//BD，需使∠ABD + ∠BAB′ = 180°， 即∠BAB′ = 110°， 由折叠的性质知∠BAF = ∠B′AF， 所以∠BAF = $\frac{1}{2}$∠BAB′ = 55°。

22. 【新考向·项目式学习试题】(2024山东济南历下期末)(12分)【阅读探究】
(1)如图1，$AB// CD$，$E$，$F$分别是$AB$，$CD$上的点，点$M$在$AB$，$CD$两平行线之间，$\angle AEM = 50^{\circ}$，$\angle CFM = 20^{\circ}$，求$\angle EMF$的度数.
解：过点$M$作$MN// AB$，
所以$\angle EMN = \angle$_______.
因为$AB// CD$，所以$MN// CD$.
所以$\angle FMN = \angle$__________.
因为$\angle AEM = 50^{\circ}$，$\angle CFM = 20^{\circ}$，
所以$\angle EMF = \angle EMN + \angle FMN = \angle AEM + \angle CFM = 50^{\circ} + 20^{\circ} = 70^{\circ}$.
(2)从(1)的推理过程中，我们发现平行线可将$\angle AEM$和$\angle CFM$“凑”在一起，得出角之间的关系，使问题得以解决. 进一步研究，我们可以发现图1中$\angle AEM$，$\angle EMF$和$\angle CFM$之间存在一定的数量关系，请直接写出它们之间的数量关系.
【方法应用】
(3)如图2，$AB// CD$，$E$，$F$分别是$AB$，$CD$上的点，点$M$在$AB$，$CD$两平行线之间，$\angle AEM = 135^{\circ}$，$\angle CFM = 155^{\circ}$，求$\angle EMF$的度数.
【应用拓展】
(4)如图3，$AB// CD$，$E$，$F$分别是$AB$，$CD$上的点，点$M$在$AB$，$CD$两平行线之间，作$\angle AEM$和$\angle CFM$的平分线$EP$，$FP$，交于点$P$(交点$P$在两平行线$AB$，$CD$之间)，若$\angle EMF = \alpha^{\circ}$，则$\angle EPF$的度数为________$^{\circ}$(用含$\alpha$的式子表示).

答案：
解析 （1）AEM；MFC。 （2）∠EMF = ∠AEM + ∠CFM。 （3）如图，过点M作MN//AB。
∵ MN//AB，∠AEM = 135°，
∴ ∠EMN = 180° - ∠AEM = 45°，
∵ AB//CD，
∴ MN//CD，
∴ ∠FMN = 180° - ∠CFM = 25°，
∴ ∠EMF = ∠EMN + ∠FMN = 45° + 25° = 70°。 （4）根据（2）得∠EMF = ∠BEM + ∠DFM = α°，
∵ EP，FP分别平分∠AEM和∠CFM，
∴ ∠AEP = $\frac{1}{2}$∠AEM = $\frac{1}{2}$(180° - ∠BEM) = 90° - $\frac{1}{2}$∠BEM，∠CFP = $\frac{1}{2}$∠CFM = $\frac{1}{2}$(180° - ∠DFM) = 90° - $\frac{1}{2}$∠DFM，
∴ ∠EPF = ∠AEP + ∠CFP = 90° - $\frac{1}{2}$∠BEM + 90° - $\frac{1}{2}$∠DFM = 180° - $\frac{1}{2}$α° = $(180 - \frac{\alpha}{2})$°。 故答案为$(180 - \frac{\alpha}{2})$。