第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
12. 如图是某公园跷跷板的简易图,$ O $ 为跷跷板 $ AB $ 的中点,支柱 $ OC $ 与地面垂直,当跷跷板 $ A $ 端着地时,$ \angle BAC = 27^{\circ} $,$ AC = 0.9m $,则 $ AB $ 的长为(
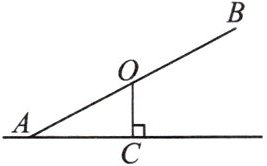
A.$ \frac{0.9}{\cos 27^{\circ}} $
B.$ \frac{1.8}{\cos 27^{\circ}} $
C.$ 1.8\cos 27^{\circ} $
D.$ \frac{1.8}{\sin 27^{\circ}} $
B
)
A.$ \frac{0.9}{\cos 27^{\circ}} $
B.$ \frac{1.8}{\cos 27^{\circ}} $
C.$ 1.8\cos 27^{\circ} $
D.$ \frac{1.8}{\sin 27^{\circ}} $
答案:
B
13. 如图,在 $ Rt\triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ BC = 5 $,$ CD \perp AB $ 于 $ D $,$ AC = 12 $,试求:
(1)$ \sin A $ 的值;
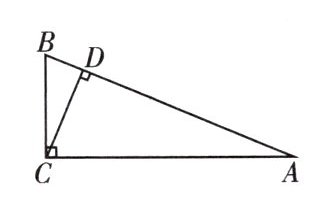
(2)$ \cos \angle ACD $ 的值;
(3)$ CD $ 的值。
(1)$ \sin A $ 的值;

(2)$ \cos \angle ACD $ 的值;
(3)$ CD $ 的值。
答案:
(1)解:由BC=5,AC=12,得AB=13,sinA=5/13.
(2)cos∠ACD=sin(90°-∠ACD)=sinA=5/13.
(3)
∵sinA=CD/AC,
∴CD=AC·sinA=12×5/13=60/13.(或由面积公式,得1/2×13×CD=1/2×12×5,解得CD=60/13.)
(1)解:由BC=5,AC=12,得AB=13,sinA=5/13.
(2)cos∠ACD=sin(90°-∠ACD)=sinA=5/13.
(3)
∵sinA=CD/AC,
∴CD=AC·sinA=12×5/13=60/13.(或由面积公式,得1/2×13×CD=1/2×12×5,解得CD=60/13.)
14. 如图,在 $ \triangle ABC $ 中,已知 $ AC = 6cm $,$ \angle C = 75^{\circ} $,$ \angle B = 45^{\circ} $,求 $ \triangle ABC $ 的面积。
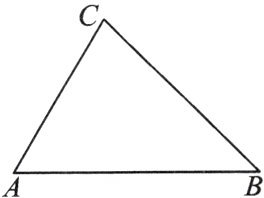

答案:
解:过点C作CD⊥AB于点D.
∵∠ACB=75°,∠B=45°,
∴∠A=60°. 则在Rt△ADC中,CD=AC·sin60°=3√3cm,AD=AC·cos60°=3cm,在Rt△BDC中,∠B=45°,BD=CD=3√3cm,
∴AB=AD+DB=(3+3√3)cm.
∴△ABC的面积为1/2AB·CD=1/2(3+3√3)×3√3=(9√3+27)/2(cm²).
∵∠ACB=75°,∠B=45°,
∴∠A=60°. 则在Rt△ADC中,CD=AC·sin60°=3√3cm,AD=AC·cos60°=3cm,在Rt△BDC中,∠B=45°,BD=CD=3√3cm,
∴AB=AD+DB=(3+3√3)cm.
∴△ABC的面积为1/2AB·CD=1/2(3+3√3)×3√3=(9√3+27)/2(cm²).
15.(核心素养·推理能力)如图,根据图中数据完成填空,再按要求答题:
$ \sin^{2}A_{1} + \cos^{2}A_{1} = $
(1)观察上述等式,猜想:在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,都有 $ \sin^{2}A + \cos^{2}A = $
(2)如图 ④,在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle A $,$ \angle B $,$ \angle C $ 的对边分别是 $ a $,$ b $,$ c $,利用三角函数的定义和勾股定理,证明你的猜想;
(3)若 $ 0^{\circ} \lt \angle A \lt 90^{\circ} $,且 $ \sin A \cdot \cos A = \frac{12}{25} $,求 $ \sin A + \cos A $ 的值。
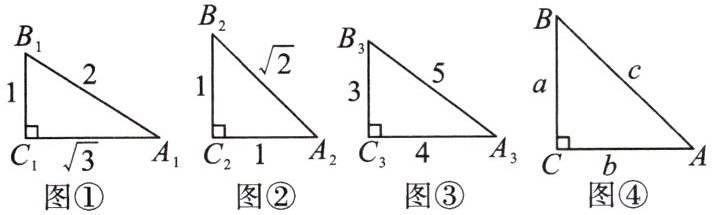
(2)证明:
∵sin²A+cos²A=(a/c)²+(b/c)²,
∴sin²A+cos²A=(a²+b²)/c²=c²/c²=1.
(3)解:
∵(sinA+cosA)²=sin²A+cos²A+2sinAcosA,
∴(sinA+cosA)²=1+24/25=49/25,
∵sinA+cosA>0,
∴sinA+cosA=7/5.
$ \sin^{2}A_{1} + \cos^{2}A_{1} = $
1
;$ \sin^{2}A_{2} + \cos^{2}A_{2} = $1
;$ \sin^{2}A_{3} + \cos^{2}A_{3} = $1
。(1)观察上述等式,猜想:在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,都有 $ \sin^{2}A + \cos^{2}A = $
1
;(2)如图 ④,在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle A $,$ \angle B $,$ \angle C $ 的对边分别是 $ a $,$ b $,$ c $,利用三角函数的定义和勾股定理,证明你的猜想;
(3)若 $ 0^{\circ} \lt \angle A \lt 90^{\circ} $,且 $ \sin A \cdot \cos A = \frac{12}{25} $,求 $ \sin A + \cos A $ 的值。

(2)证明:
∵sin²A+cos²A=(a/c)²+(b/c)²,
∴sin²A+cos²A=(a²+b²)/c²=c²/c²=1.
(3)解:
∵(sinA+cosA)²=sin²A+cos²A+2sinAcosA,
∴(sinA+cosA)²=1+24/25=49/25,
∵sinA+cosA>0,
∴sinA+cosA=7/5.
答案:
1 1 1
(1)1
(2)证明:
∵sin²A+cos²A=(a/c)²+(b/c)²,
∴sin²A+cos²A=(a²+b²)/c²=c²/c²=1.
(3)解:
∵(sinA+cosA)²=sin²A+cos²A+2sinAcosA,
∴(sinA+cosA)²=1+24/25=49/25,
∵sinA+cosA>0,
∴sinA+cosA=7/5.
(1)1
(2)证明:
∵sin²A+cos²A=(a/c)²+(b/c)²,
∴sin²A+cos²A=(a²+b²)/c²=c²/c²=1.
(3)解:
∵(sinA+cosA)²=sin²A+cos²A+2sinAcosA,
∴(sinA+cosA)²=1+24/25=49/25,
∵sinA+cosA>0,
∴sinA+cosA=7/5.
查看更多完整答案,请扫码查看


