第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. (湖南省中考改编)如图,△ABC 是等边三角形,被一平行于 BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是△ABC 的面积的(
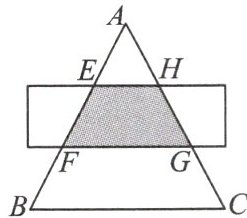
A.$ \frac{1}{9} $
B.$ \frac{2}{9} $
C.$ \frac{1}{3} $
D.$ \frac{4}{9} $
C
)
A.$ \frac{1}{9} $
B.$ \frac{2}{9} $
C.$ \frac{1}{3} $
D.$ \frac{4}{9} $
答案:
C
10. 如图,把△ABC 沿直线 AB 平移到△A’B’C’的位置,它们重叠部分(阴影部分)的面积为△ABC 面积的一半.若 $ AB = \sqrt{2} $,则此三角形移动的距离 $ AA’ $ 是
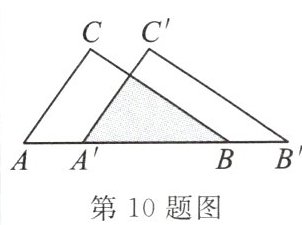
√2-1
.
答案:
√2-1
11. (辽宁省中考)如图,平行四边形 ABCD 的对角线 AC,BD 相交于点 O,过点 B 作 $ BE// AC $,交 DA 的延长线于点 E,连接 OE,交 AB 于点 F,则四边形 BCOF 的面积与△AEF 的面积的比值为
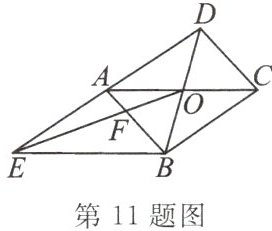
5/2
.
答案:
5/2
12. (杭州市中考改编)如图,在△ABC 中,点 D,E,F 分别在边 AB,AC,BC 上,连接 DE,EF.已知四边形 BFED 是平行四边形,$ \frac{DE}{BC}= \frac{1}{4} $.
(1)求△ADE 与△ABC 的周长比;
(2)若 $ AB = 8 $,求线段 AD 的长;
(3)若△ADE 的面积为 1,求平行四边形 BFED 的面积.
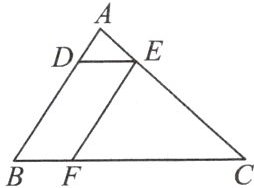
(1)求△ADE 与△ABC 的周长比;
(2)若 $ AB = 8 $,求线段 AD 的长;
(3)若△ADE 的面积为 1,求平行四边形 BFED 的面积.

答案:
(1)解:
∵四边形BFED是平行四边形,
∴DE//BF,
∴DE//BC,
∴△ADE∽△ABC,
∴C△ADE/C△ABC=DE/BC=1/4.
(2)
∵△ADE∽△ABC,
∴AD/AB=DE/BC=1/4.
∵AB=8,
∴AD=2.
(3)
∵△ADE∽△ABC,
∴S△ADE/S△ABC=(DE/BC)²=(1/4)²=1/16,AE/AC=DE/BC=1/4,即CE/AC=3/4.
∵△ADE的面积为1,
∴△ABC的面积是16.
∵四边形BFED是平行四边形,
∴EF//AB,
∴△EFC∽△ABC,
∴S△EFC/S△ABC=(CE/AC)²=(3/4)²=9/16,
∴△EFC的面积=9,
∴S□BFED=S△ABC-S△EFC-S△ADE=16-9-1=6.
(1)解:
∵四边形BFED是平行四边形,
∴DE//BF,
∴DE//BC,
∴△ADE∽△ABC,
∴C△ADE/C△ABC=DE/BC=1/4.
(2)
∵△ADE∽△ABC,
∴AD/AB=DE/BC=1/4.
∵AB=8,
∴AD=2.
(3)
∵△ADE∽△ABC,
∴S△ADE/S△ABC=(DE/BC)²=(1/4)²=1/16,AE/AC=DE/BC=1/4,即CE/AC=3/4.
∵△ADE的面积为1,
∴△ABC的面积是16.
∵四边形BFED是平行四边形,
∴EF//AB,
∴△EFC∽△ABC,
∴S△EFC/S△ABC=(CE/AC)²=(3/4)²=9/16,
∴△EFC的面积=9,
∴S□BFED=S△ABC-S△EFC-S△ADE=16-9-1=6.
13. (新考法)如图,有一边长为 5cm 的正方形 ABCD 和等腰三角形 PQR,$ PQ = PR = 5cm $,$ QR = 8cm $,点 B,C,Q,R 在同一条直线 l 上,当 C,Q 两点重合时,等腰三角形 PQR 以 1cm/s 的速度沿直线 l 按箭头所示方向开始匀速运动,t s 后正方形 ABCD 与等腰三角形 PQR 重合部分的面积为 $ S cm^2 $.当 $ t = 3 $ 时,求 S 的值.


答案:
解:过点P作PE⊥QR于点E.
∵PQ=PR,
∴QE=RE=1/2QR=4cm.
∴PE=√(5²-4²)=3(cm).当t=3时,QC=3cm.设PQ与DC交于点G.
∵PE//DC,
∴△QCG∽△QEP,
∴S△QCG/S△QEP=(3/4)².
∵S△QEP=1/2×4×3=6(cm²),
∴S=(3/4)²×6=27/8(cm²).
∵PQ=PR,
∴QE=RE=1/2QR=4cm.
∴PE=√(5²-4²)=3(cm).当t=3时,QC=3cm.设PQ与DC交于点G.
∵PE//DC,
∴△QCG∽△QEP,
∴S△QCG/S△QEP=(3/4)².
∵S△QEP=1/2×4×3=6(cm²),
∴S=(3/4)²×6=27/8(cm²).
查看更多完整答案,请扫码查看


