《2025年名校课堂内外九年级数学上册湘教版湖南专版》

1. 古希腊数学家丢番图在《算术》中提到了一元二次方程的问题,欧几里得的《原本》中记载了形如 $ x^{2}+bx = m^{2}(b ＞ 0,m ＞ 0) $ 的方程的图解法是:如图,画 $ Rt\triangle ABC $,使 $ \angle ACB = 90^{\circ} $, $ BC = \frac{b}{2} $, $ AC = m $,再在斜边 $ AB $ 上截取 $ BD = \frac{b}{2} $,则该方程的一个正实数根等于 (A)

A.$ AD $ 的长
B.$ AC $ 的长
C.$ BC $ 的长
D.$ CD $ 的长

答案： A

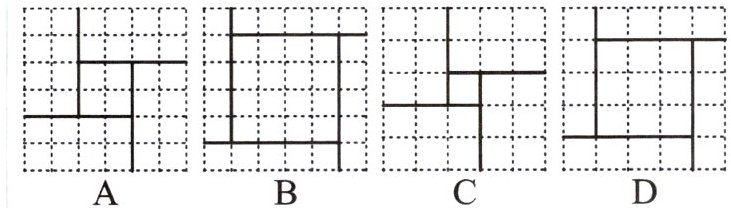
2. 三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法,以方程 $ x^{2}+2x - 35 = 0 $ 即 $ x(x + 2) = 35 $ 为例说明,记载的方法是:构造如图,大正方形的面积是 $ (x + x + 2)^{2} $.同时它又等于四个矩形的面积加上中间小正方形的面积,即 $ 4×35 + 2^{2} $,因此 $ x = 5 $.则在下面四个构图中(网格中每个小正方形边长为 1 个单位),能正确说明方程:$ x^{2}-x - 6 = 0 $ 解法的构图是 (C)

答案： C

3. 定义:如果一元二次方程 $ ax^{2}+bx + c = 0(a \neq 0) $ 满足 $ a + b + c = 0 $,那么我们称这个方程为“和谐”方程;如果一元二次方程 $ ax^{2}+bx + c = 0(a \neq 0) $ 满足 $ a - b + c = 0 $ 那么我们称这个方程为“美好”方程,如果一个一元二次方程 $ 2x^{2}+mx + n = 0 $ 既是“和谐”方程又是“美好”方程,则 $ mn $ 值为 (B)
A.2
B.0
C.-2
D.3

答案： B

4. 我们知道,一元二次方程 $ x^{2} = -1 $ 没有实数根,即不存在一个实数的平方等于 -1.若我们规定一个新数“$ i $”,使其满足 $ i^{2} = -1 $(即方程 $ x^{2} = -1 $ 有一个根为 $ i $).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有 $ i^{1} = i $, $ i^{2} = -1 $, $ i^{3} = i^{2}\cdot i = -1× i = -i $, $ i^{4} = (i^{2})^{2} = (-1)^{2} = 1 $,从而对于任意正整数 $ n $,我们可以得到 $ i^{4n + 1} = i^{4n}\cdot i = (i^{4})^{n}\cdot i = i $,同理可得 $ i^{4n + 2} = -1 $, $ i^{4n + 3} = -i $, $ i^{4n} = 1 $.那么 $ i + i^{2}+i^{3}+i^{4}+… + i^{2025} $ 的值为 (D)
A.0
B.1
C.-1
D.$ i $

答案： D

5. 【阅读理解】
【定义】如果关于 $ x $ 的方程 $ a_{1}x^{2}+b_{1}x + c_{1} = 0(a_{1} \neq 0,a_{1}、b_{1}、c_{1} $ 是常数)与 $ a_{2}x^{2}+b_{2}x + c_{2} = 0(a_{2} \neq 0,a_{2}、b_{2}、c_{2} $ 是常数),其中方程中的二次项系数、一次项系数、常数项分别满足 $ a_{1}+a_{2} = 0 $, $ b_{1} = b_{2} $, $ c_{1}+c_{2} = 0 $,则这两个方程互为“对称方程”.
【举例】求方程 $ 2x^{2}-3x + 1 = 0 $ 的“对称方程”,这样思考:由方程 $ 2x^{2}-3x + 1 = 0 $ 可知, $ a_{1} = 2 $, $ b_{1} = -3 $, $ c_{1} = 1 $,根据 $ a_{1}+a_{2} = 0 $, $ b_{1} = b_{2} $, $ c_{1}+c_{2} = 0 $,求出 $ a_{2} $, $ b_{2} $, $ c_{2} $ 就能确定这个方程的“对称方程”.请用以上方法解决下面问题:
(1)写出方程 $ x^{2}+2x + 3 = 0 $ 的“对称方程”是 $-x^{2}+2x-3=0$;
(2)若关于 $ x $ 的方程 $ 8x^{2}+(m - 3)x - n = 0 $ 与 $ -8x^{2}-x = 1 $ 互为“对称方程”,求 $ (m + n)^{2} $ 的值.

答案： （1）$-x^{2}+2x-3=0$ （2）解：由$-8x^{2}-x=1$,移项可得：$-8x^{2}-x-1=0$，
∵方程$8x^{2}+(m-3)x-n=0$与$-8x^{2}-x-1=0$互为对称方程，$\therefore m-3=-1,-n+(-1)=0$,解得：$m=2,n=-1,\therefore (m+n)^{2}=(2-1)^{2}=1.$