第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
对于二次项系数不为1的一元二次方程,先要在方程两边除以
二次项系数
,将它转化为二次项系数为1
的一元二次方程,再用上一课时所讲的配方法求解。
答案:
二次项系数 1
1. 将方程$2x^2 - 4x + 1 = 0化成(x + m)^2 = n$($m$,$n$是常数,$n\geq0$)的形式是(
A.$(x - 1)^2 = \frac{1}{2}$
B.$(x - \frac{1}{2})^2 = 1$
C.$(x - 1)^2 = 0$
D.$(x - 2)^2 = 3$
A
)A.$(x - 1)^2 = \frac{1}{2}$
B.$(x - \frac{1}{2})^2 = 1$
C.$(x - 1)^2 = 0$
D.$(x - 2)^2 = 3$
答案:
A
2. 把方程$2x^2 - 4x - 3 = 0$的二次项系数化为1,得
$x^{2}-2x-\frac {3}{2}=0$
。配方,得($x-1$
)$^2 = $$\frac {5}{2}$
。
答案:
$x^{2}-2x-\frac {3}{2}=0$ $x-1$ $\frac {5}{2}$
3. 下面是用配方法解方程$2x^2 - x - 6 = 0$的步骤,其中,开始出现错误的一步是(
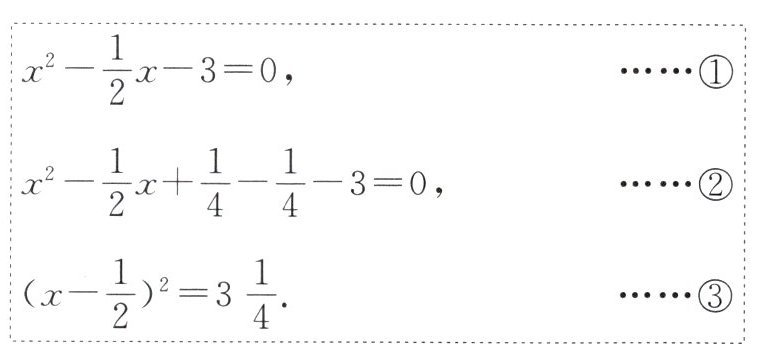
A.①
B.②
C.③
D.都正确
B
)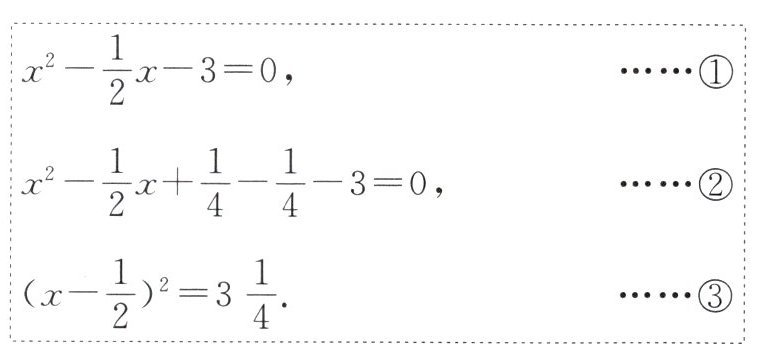
A.①
B.②
C.③
D.都正确
答案:
B
4. (答题模板)用配方法解方程:$3x^2 - 4x + 1 = 0$。
解:将二次项系数化为1,得
解:将二次项系数化为1,得
$x^{2}-\frac {4}{3}x+\frac {1}{3}=0$
。配方,得$x^2 - \frac{4}{3}x +$($\frac {2}{3}$
)$^2 -$($\frac {2}{3}$
)$^2 + \frac{1}{3} = 0$,因此,$(x -$$\frac {2}{3}$
$)^2 = $$\frac {1}{9}$
,由此得$x - \frac{2}{3} = $$\frac {1}{3}$
或$x - \frac{2}{3} = $$-\frac {1}{3}$
,解得$x_1 = $1
,$x_2 = $$\frac {1}{3}$
。
答案:
$x^{2}-\frac {4}{3}x+\frac {1}{3}=0$ $\frac {2}{3}$ $\frac {2}{3}$ $\frac {2}{3}$ $\frac {1}{9}$ $\frac {1}{3}$ $-\frac {1}{3}$ 1 $\frac {1}{3}$
5. (教材第34页例4变式)用配方法解下列方程:
(1)$\frac{1}{2}x^2 - x - 3 = 0$;
(2)$-2x^2 - 7x + 4 = 0$。
(1)$\frac{1}{2}x^2 - x - 3 = 0$;
(2)$-2x^2 - 7x + 4 = 0$。
答案:
(1)解:$x^{2}-2x=6,(x-1)^{2}=7,x-1=\pm \sqrt {7},\therefore x_{1}=1+\sqrt {7},x_{2}=1-\sqrt {7}.$
(2)解:$x^{2}+\frac {7}{2}x=2,(x+\frac {7}{4})^{2}=\frac {81}{16},x+\frac {7}{4}=\pm \frac {9}{4},\therefore x_{1}=\frac {1}{2},x_{2}=-4.$
(1)解:$x^{2}-2x=6,(x-1)^{2}=7,x-1=\pm \sqrt {7},\therefore x_{1}=1+\sqrt {7},x_{2}=1-\sqrt {7}.$
(2)解:$x^{2}+\frac {7}{2}x=2,(x+\frac {7}{4})^{2}=\frac {81}{16},x+\frac {7}{4}=\pm \frac {9}{4},\therefore x_{1}=\frac {1}{2},x_{2}=-4.$
6. 将$2x^2 - 12x + 19配方成a(x + h)^2 + k$的形式。
答案:
解:$2x^{2}-12x+19=2(x^{2}-6x)+19=2(x^{2}-6x+9-9)+19=2[(x-3)^{2}-9]+19=2(x-3)^{2}+1.$
查看更多完整答案,请扫码查看


