《2025年名校课堂内外九年级数学上册湘教版湖南专版》

8. (岳塘区模拟)《墨子·天志》记载：“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,以面积为 4 的正方形 ABCD 的中心 O 为位似中心,作它的位似图形 A'B'C'D',若 $ A'B':AB = 2:1 $,则四边形 A'B'C'D'的外接圆的面积为8π.

答案： 8π

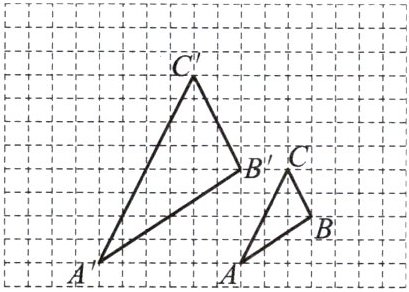
9. 如图,小方格是边长为 1 的正方形,△ABC 与△A'B'C'是以点 O 为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心 O；
(2)求△ABC 与△A'B'C'的位似比.

答案：

(1)解:根据位似图形的概念,连接$B'B,C'C$,并延长,它们相交于点O,则点O为位似图形的位似中心.如图
(2)由勾股定理,求得$AB=\sqrt{13}$,$A'B'=2\sqrt{13}$,则$\triangle ABC$与$\triangle A'B'C'$的位似比为$\frac{1}{2}$.

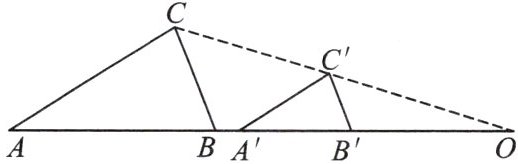
10. 如图,△ABC 与△A'B'C'是位似图形,点 A,B,A',B',O 共线,点 O 为位似中心.
(1)AC 与 A'C'平行吗？为什么？
(2)若 $ AB = 2A'B' $,$ OC' = 5 $,求 CC'的长.

答案：
(1)解:结论:AC与$A'C'$平行,理由:$\because \triangle ABC$与$\triangle A'B'C'$是位似图形,点A、B、$A'$、$B'$、O共线,$\therefore \angle A=\angle B'A'C'$,$\therefore AC// A'C'$;
(2)$\because AB=2A'B'$,$OC'=5$,$\therefore CO=2OC'=10$,$\therefore CC'$的长为:$10 - 5 = 5$.

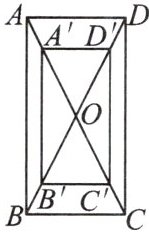
11. (核心素养·推理能力)印刷一张矩形的张贴广告如图所示,它的印刷面积(矩形 A'B'C'D')为 $ 32dm^2 $,上下空白各宽 1dm,两边空白各宽 0.5dm,设印刷部分从上到下的长为 $ x $ dm,四周空白处的面积为 $ S $ $ dm^2 $.
(1)求 S 与 x 的表达式；
(2)当要求空白处的面积为 $ 18dm^2 $ 时,求用来印刷这张广告的纸张的长和宽各是多少？
(3)在(2)的条件下,内外两个矩形是位似图形吗？如果是,请说明理由.

答案：
(1)解:$S=S_{矩形ABCD}-S_{矩形A'B'C'D'}=(\frac{32}{x}+1)(x+2)-32=x+\frac{64}{x}+2$.
(2)令$S=18$,则$x+\frac{64}{x}+2=18$,解得$x=8$,$\frac{32}{x}+1=5$,$x+2=10$,即长10dm,宽5dm.
(3)是位似图形,理由:$\because$内外两个矩形长宽比各为$\frac{8}{4}=2$和$\frac{10}{5}=2$,$\therefore \frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CD}{C'D'}=\frac{AD}{A'D'}$,且各对应点连线交于一点.$\therefore$内外两个矩形是位似图形.