《2025年名校课堂内外九年级数学上册湘教版湖南专版》

9. 点 $D$,$E$ 分别是$\triangle ABC$中 $AB$,$AC$ 边上两点,且 $AD = 4$,$BD = 2$,$AC = 8$.若$\triangle ABC与\triangle AED$相似,则 $AE$ 的长为3或$\frac{16}{3}$.

答案： 3或$\frac{16}{3}$

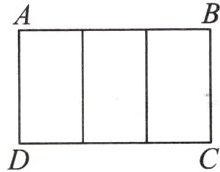
10. 如图,一块矩形 $ABCD$ 绸布的长 $AB = a$,宽 $AD = 3$,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形 $ABCD$ 绸布相似,则 $a = $$3\sqrt{3}$.

答案： $3\sqrt{3}$

11. 在下面两组图形中,每组的两个三角形相似,试分别确定$\alpha$,$x$ 的值.

答案： 解:图
(1)中,在△ABC中,∠C=180°−∠A−∠B=50°,
∴α=50°,
∵△ABC∽△A'B'C',
∴$\frac{AB}{A'B'}=\frac{AC}{A'C'}$，
∴$\frac{12}{6}=\frac{7.56}{A'C'}$，
∴A'C'=3.78，
∴x=AC=3.78. 图
(2)中,
∵∠AOB=∠COD=60°,
∴∠A=180°−∠B−∠AOB=50°,
∴α=50°,
∵△ABO∽△DCO,
∴$\frac{AB}{CD}=\frac{OB}{OC}$，
∴$\frac{AB}{12}=\frac{4}{6}$，
∴AB=8，
∴x=8.

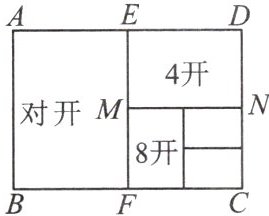
12. (临湘市期末)如图,一般书本的纸张是在原纸张多次对开的基础上得到的.矩形 $ABCD$ 沿 $EF$ 对开后,再把矩形 $EFCD$ 沿 $MN$ 对开,以此类推,如果各种开本的矩形都相似,那么 $AB$ 与 $AD$ 的比值是多少？

答案：
解:如图，在矩形ABCD中,设AD=x，AB=y，则AE=$\frac{1}{2}$AD=$\frac{1}{2}$x，
∵矩形AEFB与矩形ABCD相似，
∴$\frac{AE}{AB}=\frac{AB}{AD}$，即$\frac{\frac{1}{2}x}{y}=\frac{y}{x}$，
∴$\frac{y}{x}=\frac{\sqrt{2}}{2}$，即$\frac{AB}{AD}=\frac{\sqrt{2}}{2}$.

13. (新考法·阅读定义法)如图,我们规定菱形与正方形、矩形与正方形的接近程度为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1) 设菱形相邻两个内角的度数分别为$\alpha$,$\beta$,将菱形与正方形的“接近度”定义为$\vert\alpha - \beta\vert$,于是$\vert\alpha - \beta\vert$越小,菱形越接近于正方形.
① 若菱形的一个内角为 $80^{\circ}$,则该菱形与正方形的“接近度”为20°；
② 当菱形与正方形的“接近度”等于0°时,菱形是正方形.
(2) 设矩形的长和宽分别为 $m$,$n(m\geqslant n)$,试写出矩形与正方形的“接近度”的合理定义.

解:答案不唯一，如将矩形与正方形的“接近度”定义为$\frac{m}{n}$，$\frac{m}{n}$的值越接近1，矩形越接近于正方形.

答案：
(1)①20°　②0°
(2)解:答案不唯一，如将矩形与正方形的“接近度”定义为$\frac{m}{n}$，$\frac{m}{n}$的值越接近1，矩形越接近于正方形.