《2025年名校课堂内外九年级数学上册湘教版湖南专版》

8. 如图,不等臂跷跷板 $ AB $ 的一端 $ A $ 碰到地面时,另一端 $ B $ 到地面的高度为 $ 60cm $；当 $ AB $ 的一端 $ B $ 碰到地面时,另一端 $ A $ 到地面的高度为 $ 90cm $,则跷跷板 $ AB $ 的支撑点 $ O $ 到地面的高度 $ OH $ 是(A)

A.$ 36cm $
B.$ 40cm $
C.$ 42cm $
D.$ 45cm $

答案： A

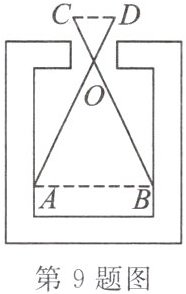
9. 如图,用一个卡钳($ AD = BC $,$\frac{OC}{OB} = \frac{OD}{OA} = \frac{1}{3}$)测量某个零件的内孔直径 $ AB $,量得 $ CD $ 长度为 $ 6cm $,则 $ AB $ 等于18cm.

答案： 18

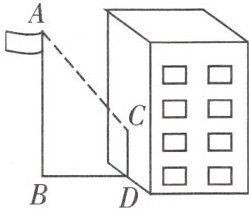
10. (新考法)某同学想测量旗杆的高度,他在某一时刻测得 $ 1 $ 米长的竹竿竖起放置时的影长为 $ 1.5 $ 米,在相同时刻测量旗杆的影长时,因旗杆靠近一栋楼房,所以影子没有全落在地面上,有一部分落在墙上,它落在地面上的影子为 $ 21 $ 米,留在墙上的影高为 $ 2 $ 米(如图所示),求旗杆的高度.

答案： 解:过 D 作 DE//CA,交 AB 于点E,则 AE=CD=2 米.由题意,知$\frac{BE}{21}=\frac{1}{1.5}$,
∴BE=14 米,
∴AB=2+14=16(米).答:旗杆的高度是 16米.

11. (项目式学习)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.

(1)如图 1,小张在测量时发现,自己在操场上的影长 $ EF $ 恰好等于自己的身高 $ DE $. 此时,小组同学测得旗杆 $ AB $ 的影长 $ BC $ 为 $ 11.3m $,据此可得旗杆高度为11.3m；
(2)如图 2,小李站在操场上 $ E $ 点处,前面水平放置镜面 $ C $,并通过镜面观测到旗杆顶部 $ A $. 小组同学测得小李的眼睛距地面高度 $ DE = 1.5m $,小李到镜面距离 $ EC = 2m $,镜面到旗杆的距离 $ CB = 16m $. 求旗杆高度；
(3)小王所在小组采用图 3 的方法测量,结果误差较大. 在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度. 方法如下：

如图 4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面 $ M $,$ N $ 两点始终处于同一水平线上.
如图 5,在支架上端 $ P $ 处,用细线系小重物 $ Q $,标高线 $ PQ $ 始终垂直于水平地面.
如图 6,在江姐故里广场上 $ E $ 点处,同学们用注水管确定与雕塑底部 $ B $ 处于同一水平线的 $ D $,$ G $ 两点,并标记观测视线 $ DA $ 与标高线交点 $ C $,测得标高 $ CG = 1.8m $,$ DG = 1.5m $. 将观测点 $ D $ 后移 $ 24m $ 到 $ D' $ 处. 采用同样方法,测得 $ C'G' = 1.2m $,$ D'G' = 2m $. 求雕塑高度(结果精确到 $ 1m $).

答案：
(1)11.3
(2)解:由反射定律可知,∠DCE=∠ACB,又∠DEC=90°=∠ABC,
∴△DEC∽△ABC,
∴$\frac{AB}{DE}=\frac{BC}{CE}$,即$\frac{AB}{1.5}=\frac{16}{2}$,解得 AB=12,
∴旗杆高度为 12 米;
(3)
∵∠CDG=∠ADB,∠CGD=90°=∠ABD,
∴△DCG∽△DAB,
∴$\frac{CG}{AB}=\frac{DG}{DB}$,设AB=x m,BD=y m,则$\frac{1.8}{x}=\frac{1.5}{y}$,
∴$y=\frac{5}{6}x$,同理可得$\frac{C'G'}{AB}=\frac{D'G'}{D'B}$,
∴$\frac{1.2}{x}=\frac{2}{24+y}$,
∴$\frac{1.2}{x}=\frac{2}{24+\frac{5}{6}x}$,解得 x=28.8;经检验,x=28.8 是原方程的解,故 AB≈29m,
∴雕塑高度 AB 约为 29m.