第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
10. 如图,在△ABC中,CD是边AB上的高,已知∠ACB= 90°,BC= 1.下列线段中,其长度为sinA的是(
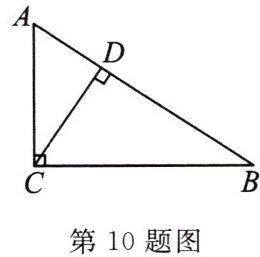
A.BD
B.AC
C.BC
D.AD
A
)
A.BD
B.AC
C.BC
D.AD
答案:
A
11. 如图,直线y= $\frac{3}{4}$x - 3与x轴、y轴分别交于A,B两点,则sin∠OAB的值为(
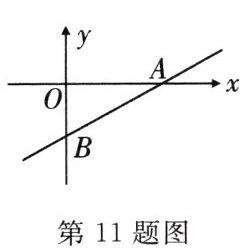
A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.-$\frac{3}{5}$
D.-$\frac{4}{5}$
A
)
A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.-$\frac{3}{5}$
D.-$\frac{4}{5}$
答案:
A
12. 如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F点.若AB:BC= 4:5,求sin∠CFD.
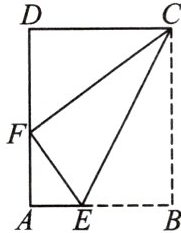

答案:
解:由折叠可知,$CB=CF$. 在矩形 $ABCD$ 中,$\because AB=CD,\therefore \sin \angle CFD$ $=\frac {CD}{CF}=\frac {AB}{BC}=\frac {4}{5}.$
13. 如图,在□ABCD中,连接BD,AD⊥BD,AB= 4,sinA= $\frac{3}{4}$,求□ABCD的面积.
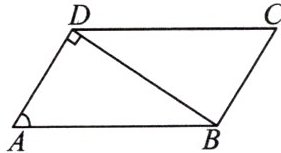

答案:
解:$\because AD\perp BD,\therefore \angle ADB=90^{\circ },\because$ $AB=4,\sin A=\frac {3}{4},\therefore BD=AB\cdot$ $\sin A=4× \frac {3}{4}=3,\therefore AD=$ $\sqrt {AB^{2}-BD^{2}}=\sqrt {4^{2}-3^{2}}=\sqrt {7},\therefore$ $S_{□ ABCD}=AD\cdot BD=3\sqrt {7}.$
14. (新考法)把含30°角的三角板ABC,绕点B逆时针旋转90°到三角板DBE位置(如图所示),求sin∠ADE的值.
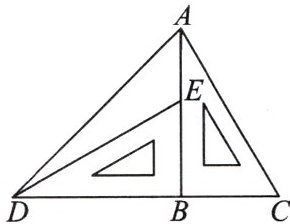

答案:
解:过点 E 作$EF\perp AD$,交 AD 于点 F,设$BE=x$,则$DE=\frac {x}{\sin 30^{\circ }}=2x,$ $BD=\sqrt {DE^{2}-BE^{2}}=\sqrt {(2x)^{2}-x^{2}}$ $=\sqrt {3}x,\therefore AB=BD=\sqrt {3}x$,在 $Rt\triangle AEF$中,$AE=AB-BE=(\sqrt {3}$ $-1)x$,易得$EF=AF=\frac {\sqrt {2}}{2}AE=$ $\frac {\sqrt {6}-\sqrt {2}}{2}x$. 在$Rt\triangle DEF$中,根据三角函数的定义可得:$\sin \angle ADE=$ $\frac {EF}{DE}=\frac {\sqrt {6}-\sqrt {2}}{4}.$
15. 如图,在4×4的正方形方格中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是

【变式】如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=

$\frac{\sqrt{5}}{5}$
。
【变式】如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC=
$\frac{\sqrt{5}}{5}$
。
答案:
$\frac{\sqrt{5}}{5}$
【变式】$\frac{\sqrt{5}}{5}$
【变式】$\frac{\sqrt{5}}{5}$
查看更多完整答案,请扫码查看


