第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 方程简化整理后只含有
一个
未知数,并且未知数的最高次数是2
的整式方程叫一元二次方程.
答案:
一个 2
2. 一元二次方程的一般形式是
$ax^{2}+bx+c=0$
(a,b,c 是已知数,a≠0),其中二次项系数是a
,一次项系数是b
,常数项是c
.
答案:
$ax^{2}+bx+c=0$ a b c
1. 下列方程是一元二次方程的是 (
A.$x^{2}-3x = 1$
B.$y^{2}-2x + 1 = 0$
C.$x^{2}+\frac{4}{x}= 0$
D.$x^{2}-2= (x + 1)^{2}$
A
)A.$x^{2}-3x = 1$
B.$y^{2}-2x + 1 = 0$
C.$x^{2}+\frac{4}{x}= 0$
D.$x^{2}-2= (x + 1)^{2}$
答案:
A
2. (邵东市期末)若关于 x 的方程$(a + 3)x^{2}+x + 4 = 0$是一元二次方程,则 a 满足的条件是 (
A.$a\neq0$
B.$a\neq - 3$
C.$a> - 3$
D.$a< - 3$
B
)A.$a\neq0$
B.$a\neq - 3$
C.$a> - 3$
D.$a< - 3$
答案:
B
3. 已知方程$3x^{3m - 1}+2 = 0$是关于 x 的一元二次方程,则$m=$
1
.
答案:
1
4. 方程$5x^{2}= 2(x - 3)$化成一般形式为
$5x^{2}-2x+6=0$
.
答案:
$5x^{2}-2x+6=0$
5. 把关于 x 的一元二次方程$(x + 1)(x - 3)= 4x^{2}-7$化为一般形式,并写出二次项系数、一次项系数和常数项.
答案:
解:$3x^{2}+2x-4=0$,二次项系数:3,一次项系数:2,常数项:-4.
6. 在方圆七百里,高七八千丈的太行、王屋两座山中开辟道路是愚公面临的最大问题.如图,有一处长为 10m,宽为 9m,地势陡峭的矩形山地,为保证安全性,在地势平坦处修建一条斜穿且面积是$30m^{2}$的道路(阴影部分),设道路的直角边长为 x m,则可列方程为 (
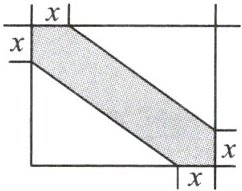
A.$(10 + x)(9 + x)= 30$
B.$(10 + x)(9 + x)= 60$
C.$(10 - x)(9 - x)= 30$
D.$(10 - x)(9 - x)= 60$
D
)
A.$(10 + x)(9 + x)= 30$
B.$(10 + x)(9 + x)= 60$
C.$(10 - x)(9 - x)= 30$
D.$(10 - x)(9 - x)= 60$
答案:
D
7. 三个连续奇数的平方和是 251,求这三个数.若设最小的奇数为 x,则可列方程为
$x^{2}+(x+2)^{2}+(x+4)^{2}=251$
.
答案:
$x^{2}+(x+2)^{2}+(x+4)^{2}=251$
8. 如图,在宽为 20m,长为 30m 的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为$500m^{2}$.若设路宽为 x m,列出方程,并将其化成一元二次方程的一般形式.
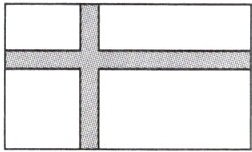

答案:
解:耕地的长为$(30-x)m$,宽为$(20-x)m$,根据面积公式可得:$(30-x)(20-x)=500$.整理得出:$x^{2}-50x+100=0$.
9. (武陵区期末)已知$(m - 1)x^{m^{2}+1}-3x + 1 = 0$是关于 x 的一元二次方程,则$m=$
-1
.
答案:
-1
查看更多完整答案,请扫码查看


