《2025年名校课堂内外九年级数学上册湘教版湖南专版》

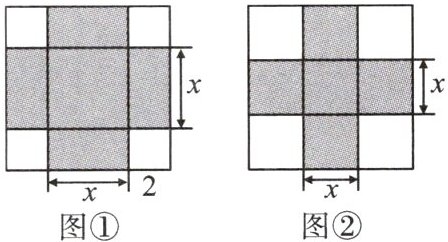
10. (解题方法型阅读理解题)《代数学》中有记载,形如$x^{2}+8x= 33$的方程,求正数解的几何方法是：“如图①,先构造一个面积为$x^{2}$的正方形,再以正方形的边为一边向外构造四个面积为$\frac{8}{4}x = 2x$的长方形,得到大正方形的面积为$33+2^{2}×4 = 49$,则该方程的正数解为$\sqrt{49}-2×2 = 3$。”若按此方法解关于$x的方程x^{2}+20x+p = 0$时,构造出如图②所示的图形,已知阴影部分的面积为125。则该方程的正数解是5。

答案： 5

11. 用配方法解下列方程：
(1)$x^{2}-3x - 10= 0$；
(2)$(x - 2)(x + 3)= 6$。

答案：
(1)解:$x^{2}-3x+(\frac {3}{2})^{2}-(\frac {3}{2})^{2}-10=0,(x-\frac {3}{2})^{2}=\frac {49}{4},x-\frac {3}{2}=\frac {7}{2}$或$x-\frac {3}{2}=-\frac {7}{2},\therefore x_{1}=5,x_{2}=-2$.
(2)解:$x^{2}+x-6=6,x^{2}+x=12,(x+\frac {1}{2})^{2}=\frac {49}{4},\therefore x_{1}=3,x_{2}=-4.$

12. 一元二次方程$x^{2}-2x-\frac{5}{4}= 0$的某个根,也是一元二次方程$x^{2}-(k + 2)x+\frac{9}{4}= 0$的根,求$k$的值。

答案： 解:把$x^{2}-2x-\frac {5}{4}=0$配方得$(x-1)^{2}=\frac {9}{4}.\therefore x-1=\pm \frac {3}{2}.\therefore x_{1}=\frac {5}{2},x_{2}=-\frac {1}{2}$.把$x_{1}=\frac {5}{2}$代入$x^{2}-(k+2)x+\frac {9}{4}=0$,解得$k=\frac {7}{5}$;把$x_{2}=-\frac {1}{2}$代入$x^{2}-(k+2)x+\frac {9}{4}=0$,解得$k=-7.\therefore k=\frac {7}{5}$或$k=-7.$

13. (临湘市期末)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。例如：
求代数式$x^{2}+4x+5$的最小值。
解答过程如下：
解：$x^{2}+4x+5= (x^{2}+4x+4)+1= (x+2)^{2}+1$
$\because(x + 2)^{2}\geq0$,$\therefore(x + 2)^{2}+1\geq1$,
$\therefore当x = - 2$时,$x^{2}+4x+5$有最小值,是1。
(1)仿照上述方法,求代数式$x^{2}-6x+12$的最小值；
(2)$-x^{2}+8x - 1$有最大(选填“大”或“小”)值,是15。
(1)解:$x^{2}-6x+12=(x^{2}-6x+9)+3=(x-3)^{2}+3,\because (x-3)^{2}≥0,\therefore (x-3)^{2}+3≥3$,
∴当$x=3$时,代数式$x^{2}-6x+12$有最小值,是3.

答案：
(1)解:$x^{2}-6x+12=(x^{2}-6x+9)+3=(x-3)^{2}+3,\because (x-3)^{2}≥0,\therefore (x-3)^{2}+3≥3$,
∴当$x=3$时,代数式$x^{2}-6x+12$有最小值,是3.
(2)大 15