《2025年名校课堂内外九年级数学上册湘教版湖南专版》

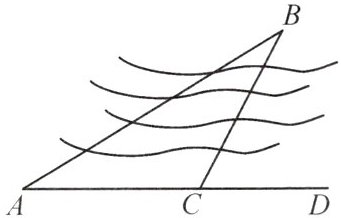
12.(数学应用)如图,要测量B点到河岸AD的距离,在A点测得∠BAD = 30°,在C点测得∠BCD = 60°,又测得AC = 100米,则B点到河岸AD的距离为$50\sqrt{3}$米。

答案： $50\sqrt{3}$

13. 计算：
(1)$\frac{1}{2}\sin 60^{\circ}+\frac{\sqrt{2}}{2}\sin 45^{\circ}+\sin 30^{\circ}\sin 60^{\circ}+2\sin 60^{\circ}$；
(2)$\sqrt{2}×\sqrt{6}+4×|1-\sqrt{3}|\sin 60^{\circ}-(\frac{1}{2})^{-1}$。

答案：
(1)解:原式$=\frac{1}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}+\frac{1}{2}×\frac{\sqrt{3}}{2}+2×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}+\frac{1}{2}+\frac{\sqrt{3}}{4}+\sqrt{3}=\frac{3}{2}\sqrt{3}+\frac{1}{2}$。
(2)解:原式$=2\sqrt{3}+4×(\sqrt{3}-1)×\frac{\sqrt{3}}{2}-2=2\sqrt{3}+2\sqrt{3}×(\sqrt{3}-1)-2=2\sqrt{3}+6 - 2\sqrt{3}-2 = 4$。

14. 已知∠A,∠B是△ABC中的两个锐角,且$(\sin A-\frac{1}{2})^{2}+|\sin B-\frac{\sqrt{2}}{2}|= 0$,求∠C的度数。

答案： 解:$\because(\sin A - \frac{1}{2})^{2}+\left|\sin B - \frac{\sqrt{2}}{2}\right| = 0$，$\therefore\sin A=\frac{1}{2}$，$\sin B=\frac{\sqrt{2}}{2}$。$\because\angle A$，$\angle B$是$\triangle ABC$中的两个锐角，$\therefore\angle A = 30^{\circ}$，$\angle B = 45^{\circ}$，$\therefore\angle C = 180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$。

15. 在Rt△ABC中,∠C = 90°,a,b,c分别是∠A,∠B,∠C的对边。
(1)已知$c = 2\sqrt{3}$,$b = \sqrt{6}$,求∠B；
(2)已知c = 12,$\sin A= \frac{1}{2}$,求b。

答案：
(1)解:$\because\sin B=\frac{b}{c}=\frac{\sqrt{6}}{2\sqrt{3}}=\frac{\sqrt{2}}{2}$，$\therefore\angle B = 45^{\circ}$；
(2)$\because\sin A=\frac{1}{2}$，$\therefore\angle A = 30^{\circ}$，$\therefore\angle B = 60^{\circ}$，$\sin B=\frac{b}{12}=\frac{\sqrt{3}}{2}$，$\therefore b = 6\sqrt{3}$。

16.(转化思想)如图,网格中所有小正方形的边长均为1,点A,B,C,D都是小正方形的顶点,AB与CD相交于点P,求$\sin \angle BPD$的值。

答案：
解:如图，连接$AE$，$BE$，$AC = ED = 1$，$AC// ED$，$\therefore$四边形$AEDC$是平行四边形，$\therefore AE// CD$，$\therefore\angle BAE=\angle BPD$。$\because BE = AE=\sqrt{3^{2}+1^{2}}=\sqrt{10}$，$AB=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$，$\therefore AE^{2}+BE^{2}=AB^{2}$，$\therefore\triangle AEB$是等腰直角三角形，$\therefore\angle EAB=\angle BPD = 45^{\circ}$，$\therefore\sin\angle BPD=\sin45^{\circ}=\frac{\sqrt{2}}{2}$。