《2025年名校课堂内外九年级数学上册湘教版湖南专版》

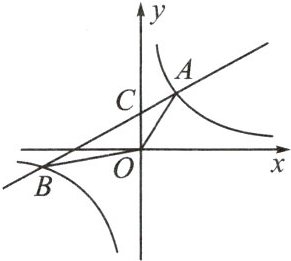
【母题】如图,一次函数 $ y = k_1x + b(k_1 \neq 0) $ 与反比例函数 $ y = \frac{k_2}{x}(k_2 \neq 0) $ 的图象交于点 $ A(2,3) $,$ B(n,-1) $,与 $ y $ 轴交于点 $ C $.
(1)求反比例函数和一次函数的表达式；
(2)求 $ \triangle AOB $ 的面积；
(3)直接写出不等式 $ k_1x + b \geq \frac{k_2}{x} $ 的解集.

答案： 【母题】
(1)解：将A(2,3)代入y=xk2​​，得3=2k2​​，解得k2​=6。
∴y=x6​。把B(n,-1)代入y=x6​，得−1=n6​，解得n=−6。
∴点B的坐标为(-6,-1)。把A(2,3)，B(-6,-1)代入y=k1​x+b，得{3=2k1​+b−1=−6k1​+b​，解得{k1​=21​b=2​，
∴y=21​x+2。
(2)把x=0代入y=21​x+2，得y=2，
∴C(0,2)。
∴S△AOB​=S△AOC​+S△BOC​=21​∣yC​∣⋅∣xA​∣+21​∣yC​∣⋅∣xB​∣=21​×2×2+21​×2×6=8。
(3)x≥2或−6≤x<0。

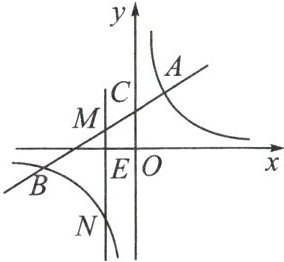
【变式设问 1】如图,$ MN \perp x $ 轴于点 $ E $,分别交上述一次函数与反比例函数的图象于点 $ M $,$ N $.当 $ OE = 1 $ 时,求线段 $ MN $ 的长.

答案： 【变式设问 1】解：
∵MN⊥x轴，
∴MN//y轴，
∵OE=1，
∴点M，N的横坐标为-1。
∴M(−1,23​)，N(−1,−6)。
∴MN=23​+6=215​。

【变式设问 2】过点 $ A $ 作 $ AD \perp x $ 轴于点 $ D $,若点 $ P $ 在双曲线 $ y = \frac{k_2}{x}(k_2 \neq 0) $ 上,且 $ \triangle PAD $ 的面积为 $ 6 $,求点 $ P $ 的坐标.

答案： 【变式设问 2】解：设点P的坐标为(a,a6​)。
∵A(2,3)，
∴D(2,0)。
∵△PAD的面积为6。
∴21​AD⋅∣2−a∣=6。即21​×3⋅∣2−a∣=6，解得a=−2或a=6。
∴P(−2,−3)或(6,1)。

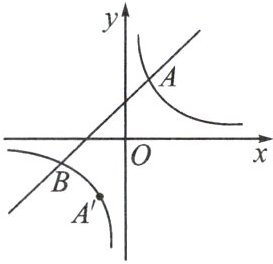
【变式设问 3】如图,点 $ A $ 关于原点 $ O $ 的对称点为 $ A' $,在 $ x $ 轴上找一点 $ P $,使 $ PA' + PB $ 最小,求出点 $ P $ 的坐标.

答案： 【变式设问 3】解：作点B关于x轴的对称点B′，连接A′B′交x轴于点P。
∵点A(2,3)，点A与点A′关于原点O对称，
∴点A′的坐标为(-2,-3)。又
∵点B(-6,-1)，点B和点B′关于x轴对称，
∴点B′的坐标为(-6,1)。设直线A′B′表达式为y=kx+b，将点A′(−2,−3)，B′(−6,1)代入y=kx+b，得{−2k+b=−3−6k+b=1​，解得{k=−1b=−5​，
∴直线A′B′的表达式为y=−x−5。对于y=−x−5，当y=0时，x=−5，
∴点P的坐标为(-5,0)。