第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
8. 在 $ \triangle ABC $ 中,$ AB = 6 $,$ AC = 9 $,点 $ P $ 是直线 $ AB $ 上一点,且 $ AP = 2 $,过点 $ P $ 作 $ BC $ 边的平行线,交直线 $ AC $ 于点 $ M $,则 $ MC $ 的长为
6 或 12
.
答案:
6 或 12
9. (北海市期末)如图,嘉嘉要测量池塘两岸 $ A $,$ B $ 两点间的距离,先在 $ AB $ 的延长线上选一定点 $ C $,测得 $ BC = 5m $,再选一点 $ D $,连接 $ AD $,$ CD $,作 $ BE // AD $,交 $ CD $ 于点 $ E $,测得 $ CD = 8m $,$ DE = 4m $,则 $ AB = $ (
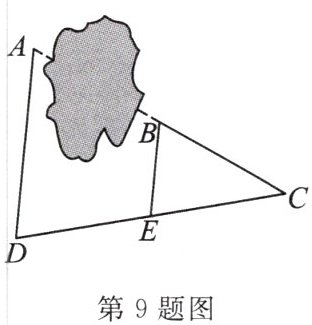
A.$ 3m $
B.$ 4m $
C.$ 5m $
D.$ 6m $
C
)
A.$ 3m $
B.$ 4m $
C.$ 5m $
D.$ 6m $
答案:
C
10. (郴州市中考)如图是一架梯子的示意图,其中 $ AA_1 // BB_1 // CC_1 // DD_1 $,且 $ AB = BC = CD $. 为使其更稳固,在 $ A $,$ D_1 $ 间加绑一条安全绳 (线段 $ AD_1 $),量得 $ AE = 0.4m $,则 $ AD_1 = $
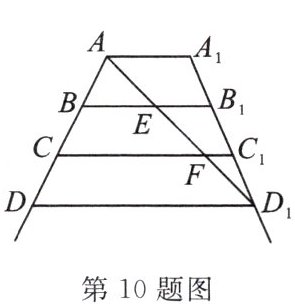
1.2
$ m $.
答案:
1.2
11. 如图,$ DE // BC $,$ DF // AC $,$ AD = 4cm $,$ BD = 8cm $,$ DE = 5cm $,求线段 $ BF $ 的长.
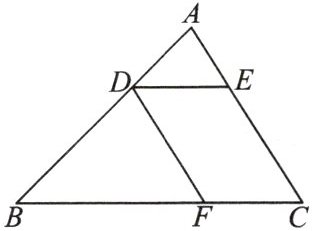

答案:
解:$\because DE// BC,DF// AC,\therefore$ 四边形 DFCE 是平行四边形,$\therefore CF=DE=5cm.\because DF// AC,\therefore \frac{BF}{CF}=\frac{BD}{AD},\therefore BF=\frac{CF\cdot BD}{AD}=10cm.$
12. (贵州省中考改编)如图,已知 $ DE // BC $,$ FE // CD $,$ AF = 3 $,$ AD = 5 $,$ AE = 4 $.
(1) 求 $ CE $ 的长;
(2) 求 $ AB $ 的长.
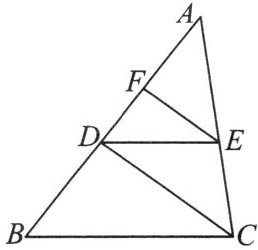
(1) 求 $ CE $ 的长;
(2) 求 $ AB $ 的长.

答案:
(1)解:$\because FE// CD,\therefore \frac{AE}{AC}=\frac{AF}{AD}$,即 $\frac{4}{AC}=\frac{3}{5}$,解得 $AC=\frac{20}{3}$,则 $CE=AC-AE=\frac{20}{3}-4=\frac{8}{3}$;
(2)$\because DE// BC,\therefore \frac{AD}{AB}=\frac{AE}{AC}=\frac{AF}{AD}$,即 $\frac{5}{AB}=\frac{3}{5}$,解得 $AB=\frac{25}{3}.$
(1)解:$\because FE// CD,\therefore \frac{AE}{AC}=\frac{AF}{AD}$,即 $\frac{4}{AC}=\frac{3}{5}$,解得 $AC=\frac{20}{3}$,则 $CE=AC-AE=\frac{20}{3}-4=\frac{8}{3}$;
(2)$\because DE// BC,\therefore \frac{AD}{AB}=\frac{AE}{AC}=\frac{AF}{AD}$,即 $\frac{5}{AB}=\frac{3}{5}$,解得 $AB=\frac{25}{3}.$
如图,$ AD $ 是 $ \triangle ABC $ 的中线.
(1) 若 $ E $ 为 $ AD $ 的中点,射线 $ CE $ 交 $ AB $ 于点 $ F $,$ \frac{AF}{BF} $ 的值为
(2) 若 $ E $ 为 $ AD $ 上的一点,且 $ \frac{AE}{ED} = \frac{1}{k} $,射线 $ CE $ 交 $ AB $ 于点 $ F $,则 $ \frac{AF}{BF} $ 的值为
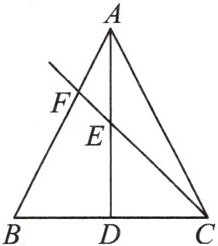
(1) 若 $ E $ 为 $ AD $ 的中点,射线 $ CE $ 交 $ AB $ 于点 $ F $,$ \frac{AF}{BF} $ 的值为
$\frac{1}{2}$
;(2) 若 $ E $ 为 $ AD $ 上的一点,且 $ \frac{AE}{ED} = \frac{1}{k} $,射线 $ CE $ 交 $ AB $ 于点 $ F $,则 $ \frac{AF}{BF} $ 的值为
$\frac{1}{2k}$
.
答案:
(1)$\frac{1}{2}$
(2)$\frac{1}{2k}$
(1)$\frac{1}{2}$
(2)$\frac{1}{2k}$
如图,在 $ \triangle ABC $ 中,$ D $ 在 $ AC $ 边上,$ AD:DC = 1:2 $,$ O $ 是 $ BD $ 的中点,连接 $ AO $ 并延长交 $ BC $ 于 $ E $,则 $ BE:EC = $
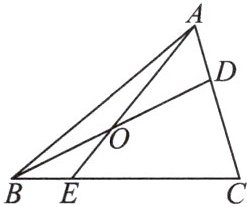
1:3
.
答案:
1:3
查看更多完整答案,请扫码查看


