第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图,为了测量一池塘的宽 $ DE $,在岸边找一点 $ C $,测得 $ CD = 30m $,在 $ DC $ 的延长线上找一点 $ A $,测得 $ AC = 5m $,过点 $ A $ 作 $ AB // DE $,交 $ EC $ 的延长线于点 $ B $,测得 $ AB = 6m $,则池塘的宽 $ DE $ 为(

A.$ 25m $
B.$ 30m $
C.$ 36m $
D.$ 50m $
C
)
A.$ 25m $
B.$ 30m $
C.$ 36m $
D.$ 50m $
答案:
C
2. (武冈市期末)如图,为估算某河的宽度,在河对岸,选定一个目标点 $ A $,在近岸取点 $ B $,$ C $,$ D $,使得 $ AB \perp BC $,$ CD \perp BC $,点 $ E $ 在 $ BC $ 上,并且点 $ A $,$ E $,$ D $ 在同一条直线上. 若测得 $ BE = 20m $,$ CE = 10m $,$ CD = 20m $,则河的宽度 $ AB $ 等于
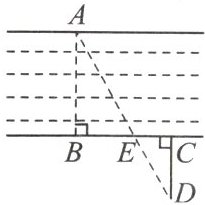
40m
.
答案:
40m
3. 如图,某校宣传栏 $ BC $ 后面 $ 12 $ 米处种有一排与宣传栏平行的若干棵树,即 $ BC // ED $,且相邻两棵树的间隔为 $ 2 $ 米,一人站在宣传栏前面的 $ A $ 处正好看两端的树干,其余的树均被宣传栏挡住. 已知 $ AF \perp BC $,$ AF = 3 $ 米,$ BC = 10 $ 米,求该宣传栏后 $ DE $ 段共有多少棵树?(不计宣传栏的厚度)
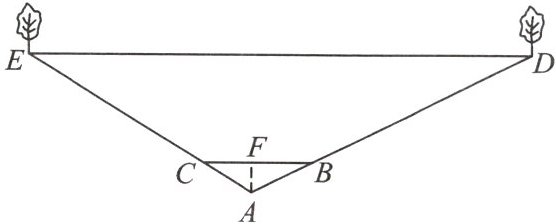

答案:
解:延长 AF 交 ED 于点 G,易证 AG⊥DE.
∵BC//ED,
∴△ABC∽△ADE,
∴$\frac{AF}{AG}=\frac{BC}{DE}$.
∵BC=10 米,AF=3 米,FG=12 米,
∴AG=AF+FG=15(米),
∴$\frac{3}{15}=\frac{10}{DE}$.
∴DE=50米.50÷2=25,25+1=26(棵).答:DE 段共有 26 棵树.
∵BC//ED,
∴△ABC∽△ADE,
∴$\frac{AF}{AG}=\frac{BC}{DE}$.
∵BC=10 米,AF=3 米,FG=12 米,
∴AG=AF+FG=15(米),
∴$\frac{3}{15}=\frac{10}{DE}$.
∴DE=50米.50÷2=25,25+1=26(棵).答:DE 段共有 26 棵树.
4. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端. 已知小菲的眼睛离地面高度为 $ 1.6m $,同时量得小菲与镜子的水平距离为 $ 2m $,镜子与旗杆的水平距离为 $ 10m $,则旗杆高度为(
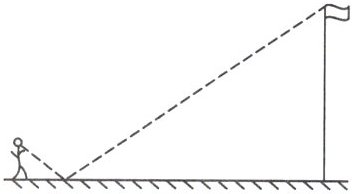
A.$ 6.4m $
B.$ 8m $
C.$ 9.6m $
D.$ 12.5m $
B
)
A.$ 6.4m $
B.$ 8m $
C.$ 9.6m $
D.$ 12.5m $
答案:
B
5. (广西自治区中考)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度. 如图,木杆 $ EF $ 长 $ 2 $ 米,它的影长 $ FD $ 是 $ 4 $ 米,同一时刻测得 $ OA $ 是 $ 268 $ 米,则金字塔的高度 $ BO $ 是
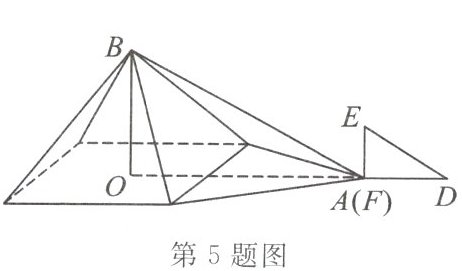
134
米.
答案:
134
6. 在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,$ AB $ 表示塔的高度,$ CD $ 表示竹竿顶端到地面的高度,$ EF $ 表示人眼到地面的高度,$ AB $、$ CD $、$ EF $ 在同一平面内,点 $ A $、$ C $、$ E $ 在一条水平直线上. 已知 $ AC = 20 $ 米,$ CE = 10 $ 米,$ CD = 7 $ 米,$ EF = 1.4 $ 米,人从点 $ F $ 远眺塔顶 $ B $,视线恰好经过竹竿的顶端 $ D $,可求出塔的高度. 根据以上信息,塔的高度为
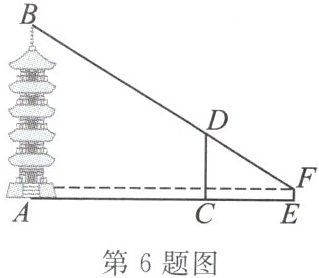
18.2
米.
答案:
18.2
7. 如图,点 $ D $,$ E $ 分别在 $ AC $,$ BC $ 上,如果测得 $ CD = 20m $,$ CE = 40m $,$ AD = 100m $,$ BE = 20m $,$ DE = 45m $,则 $ A $,$ B $ 两地间的距离为
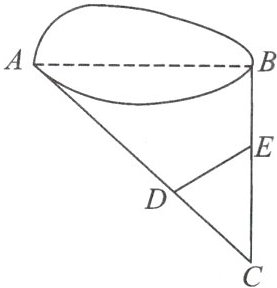
135
m.
答案:
135
查看更多完整答案,请扫码查看


