《2025年名校课堂内外九年级数学上册湘教版湖南专版》

9. 如果一个直角三角形的两条边长分别是$6和8$,另一个与它相似的直角三角形边长分别是$3$,$4及x$,那么$x$的值为$\sqrt{7}$或 5.

答案： $\sqrt{7}$或 5

10. 如图,已知$\frac{AB}{AD}= \frac{BC}{DE}= \frac{AC}{AE}$,点$B$,$D$,$F$,$E$在同一条直线上,请找出图中的相似三角形,并说明理由.

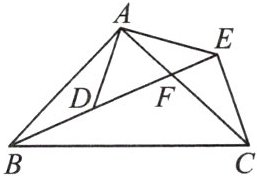
答案： 解:△ABC∽△ADE,△BAD∽△CAE. 理由:
∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,
∴△ABC∽△ADE,
∴∠BAC=∠DAE.
∴∠BAD=∠CAE.
∵$\frac{AB}{AD}=\frac{AC}{AE}$,即$\frac{AB}{AC}=\frac{AD}{AE}$,
∴△BAD∽△CAE.

11. (数学推理)已知一个三角形框架的三边长分别为$3\mathrm{m}$,$4\mathrm{m}$,$5\mathrm{m}$,现要做一个与其相似的三角形框架,已有一根长为$2\mathrm{m}$的木条,问其他两根木条可选多长？共有多少种不同选法？

答案： 解:共有三种选法.①若 2 米的木条为最短边,设其他两根木条的长为x 米和 y 米,则$\frac{3}{2}=\frac{4}{x}=\frac{5}{y}$.解得 x=$\frac{8}{3}$,y=$\frac{10}{3}$. ②若 2 米长的木条为第二长的边长,设其他两根木条的长分别为 x 米和 y 米,则$\frac{3}{x}=\frac{4}{2}=\frac{5}{y}$,解得 x=$\frac{3}{2}$,y=$\frac{5}{2}$. ③若 2米长的木条为最长边,设其他两根木条的长分别为 x 米和 y 米.则$\frac{3}{x}=\frac{4}{y}=\frac{5}{2}$,解得 x=$\frac{6}{5}$,y=$\frac{8}{5}$.

12. 如图,在边长为$1$的小正方形组成的网格中,$\triangle ABC和\triangle DEF$的顶点都在格点上,$P_{1}$、$P_{2}$、$P_{3}$、$P_{4}$、$P_{5}是\triangle DEF边上的5$个格点,请按要求完成下列各题：
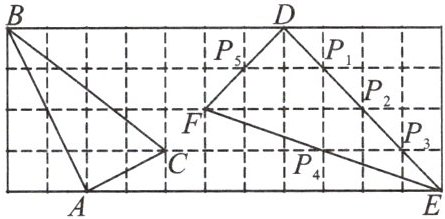
(1)试证明$\triangle ABC$为直角三角形；
(2)判断$\triangle ABC和\triangle DEF$是否相似,并说明理由；
(3)直接写出一个与$\triangle ABC$相似的三角形,使它的三个顶点为$P_{1}$、$P_{2}$、$P_{3}$、$P_{4}$、$P_{5}$中的三个格点. 并说明理由.

答案： （1)证明:由勾股定理得:$AB^{2}=2^{2}+4^{2}=20$,$AC^{2}=2^{2}+1^{2}=5$,$BC^{2}=3^{2}+4^{2}=25$,即$AB^{2}+AC^{2}=BC^{2}$,所以△ABC 是直角三角形；（2）解：相似,理由是:由勾股定理得:$DF=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$,$DE=\sqrt{4^{2}+4^{2}}=4\sqrt{2}$,$EF=\sqrt{2^{2}+6^{2}}=2\sqrt{10}$,由（1)知:$AB=2\sqrt{5}$,$AC=\sqrt{5}$,$BC=5$,所以$\frac{DF}{AC}=\frac{DE}{AB}=\frac{EF}{BC}=\frac{2\sqrt{10}}{5}$,所以△ABC∽△DEF；（3）解：和△ABC 相似的三角形是△P₂P₄P₅,理由是:由勾股定理得:$P_{5}P_{2}=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,$P_{2}P_{4}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$,$P_{4}P_{5}=2\sqrt{2}$,又
∵$AB=2\sqrt{5}$,$AC=\sqrt{5}$,$BC=5$,
∴$\frac{AC}{P_{2}P_{4}}=\frac{AB}{P_{5}P_{4}}=\frac{BC}{P_{5}P_{2}}=\frac{\sqrt{10}}{2}$,
∴△ABC∽△P₄P₅P₂.