《2025年名校课堂内外九年级数学上册湘教版湖南专版》

9. 若$\frac{a}{b}= \frac{c}{d}$($a$,$b$,$c$,$d$均不为零),则下列式子一定成立的是(D)
A.$\frac{c}{a}= \frac{b}{d}$
B.$\frac{a + 1}{b + 1}= \frac{c + 1}{d + 1}$
C.$\frac{a - d}{b}= \frac{c - b}{d}$
D.$\frac{a + 4b}{b}= \frac{c + 4d}{d}$

答案： D

10. (1)若$\frac{a}{a + b}= \frac{1}{3}$,则$\frac{b}{a}=$2；
(2)若$\frac{b}{a - b}= \frac{3}{4}$,则$\frac{a}{b}=$$\frac{7}{3}$。

答案：
(1)2
(2)$\frac{7}{3}$

11. (岳塘区期末)已知$\frac{x}{3}= \frac{y}{4}= \frac{z}{5}$($x\neq0$),则$\frac{x - y + z}{x}= $$\frac{4}{3}$。

答案： $\frac{4}{3}$

12. 已知$\frac{b}{a}= \frac{c}{d}\neq1$。求证：$\frac{b + a}{b - a}= \frac{c + d}{c - d}$。

答案： 证明:设$\frac{b}{a}=\frac{c}{d}=k(k≠1)$,则b=ak,c=dk.将其代入左右两边,可得:左边=$\frac{ak+a}{ak-a}=\frac{k+1}{k-1}$,右边=$\frac{dk+d}{dk-d}=\frac{k+1}{k-1}$.
∵左边=右边,
∴$\frac{b+a}{b-a}=\frac{c+d}{c-d}$.

13. (核心素养·应用意识)《九章算术》中记载,战国时期的铜衡杆,其形式既不同于天平衡杆,也异于称杆。衡杆正中有拱肩提纽和穿线孔,一面刻有贯通上、下的十等分线。用该衡杆称物,可以把被称物与砝码放在提纽两边不同位置的刻线上,这样,用同一个砝码就可以称出大于它一倍或几倍重量的物体。图为铜衡杆的使用示意图,此时被称物重量是砝码重量的多少倍？

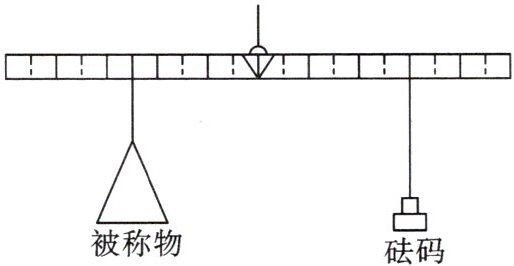
答案： 解:由题意得,$5m_{被称物}=6m_{砝码}$,
∴$m_{被称物}:m_{砝码}=6:5=1.2$.故此时被称物重量是砝码重量的1.2倍.

【变式 1】已知$\frac{a}{2}= \frac{b}{3}= \frac{c}{4}$,且$2a - b + c = 10$,则$a + b - 2c= $-6。

答案： -6

【变式 2】已知$a:b:c = 2:3:5$,求$\frac{a - 2b + c}{3a - c}$的值。

答案： 解:
∵a:b:c=2:3:5,
∴设a=2k,b=3k,c=5k(k≠0),则$\frac{a-2b+c}{3a-c}=\frac{2k-2×3k+5k}{3×2k-5k}=1$.

【变式 3】设$a$,$b$,$c是\triangle ABC$的三条边,且$\frac{a - b}{b}= \frac{b - c}{c}= \frac{c - a}{a}$,则$\triangle ABC$的形状是(D)
A.等腰三角形
B.等腰直角三角形
C.直角三角形
D.等边三角形

答案： D