第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 相似三角形的面积比等于相似比的
平方
.
答案:
平方
2. 相似三角形的周长比等于相似比.
答案:
相似三角形的周长比等于相似比。
1. 如图,在△ABC 中,点 D,E 分别为 AB,AC 的中点,则 $ S_{△ADE}:S_{△ABC}= $ (
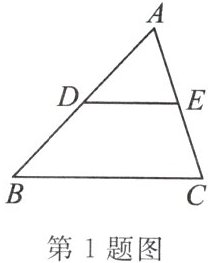
A.$ 1:1 $
B.$ 1:2 $
C.$ 1:3 $
D.$ 1:4 $
D
)
A.$ 1:1 $
B.$ 1:2 $
C.$ 1:3 $
D.$ 1:4 $
答案:
D
2. (广西自治区中考改编)如图,四边形 ABCD 为平行四边形,E,F 为 CD 边的两个三等分点,连接 AF,BE,交于点 G,则 $ S_{△EFG}:S_{△ABG}= $
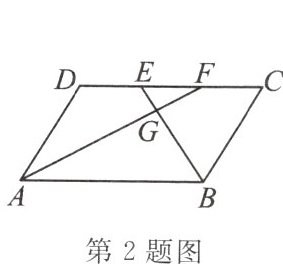
1:9
.
答案:
1:9
3. (岳阳楼区期末)如图,在△ABC 和△DEC 中,$ ∠BCE= ∠ACD $,$ ∠B= ∠CED $.
(1)求证:$ △ABC∽△DEC $;
(2)若 $ S_{△ABC}:S_{△DEC}= 4:9 $,$ BC= 3 $,求 EC 的长.
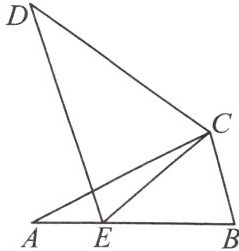
(1)求证:$ △ABC∽△DEC $;
(2)若 $ S_{△ABC}:S_{△DEC}= 4:9 $,$ BC= 3 $,求 EC 的长.

答案:
(1)证明:
∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
∵∠B=∠CED,
∴△ABC∽△DEC;
(2)解:由
(1)得,△ABC∽△DEC,
∵S△ABC:S△DEC=4:9,
∴S△ABC/S△DEC=4/9=(BC/EC)²,
∵BC=3,
∴EC=9/2.
(1)证明:
∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
∵∠B=∠CED,
∴△ABC∽△DEC;
(2)解:由
(1)得,△ABC∽△DEC,
∵S△ABC:S△DEC=4:9,
∴S△ABC/S△DEC=4/9=(BC/EC)²,
∵BC=3,
∴EC=9/2.
4. 已知△ABC 与△DEF 相似,且相似比为 $ 1:3 $,则△ABC 与△DEF 的周长之比是 (
A.$ 1:1 $
B.$ 1:3 $
C.$ 1:6 $
D.$ 1:9 $
B
)A.$ 1:1 $
B.$ 1:3 $
C.$ 1:6 $
D.$ 1:9 $
答案:
B
5. 如图,AB 与 CD 交于点 O,且 $ AC// BD $.若 $ \frac{OA + OC + AC}{OB + OD + BD}= \frac{1}{2} $,则 $ \frac{AC}{BD}= $
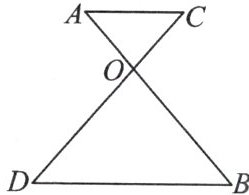
1/2
.
答案:
1/2
6. 两个相似三角形的面积比为 $ 9:25 $,则它们的周长比为
3:5
.
答案:
3:5
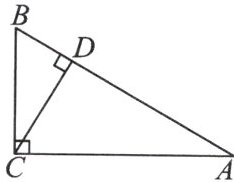
7. 如图,在 $ Rt△ABC $ 中,$ ∠ACB = 90° $,$ BC = 1 $,$ AB = 2 $,$ CD⊥AB $ 于点 D,求△BCD 与△ABC 的周长之比.

答案:
解:
∵CD⊥AB,
∴∠CDB=90°,又
∵∠ACB=90°,
∴∠CDB=∠ACB,
∵∠B=∠B,
∴△BCD∽△BAC,
∴C△BCD/C△BAC=BC/BA=1/2,故△BCD与△ABC的周长之比为1:2.
∵CD⊥AB,
∴∠CDB=90°,又
∵∠ACB=90°,
∴∠CDB=∠ACB,
∵∠B=∠B,
∴△BCD∽△BAC,
∴C△BCD/C△BAC=BC/BA=1/2,故△BCD与△ABC的周长之比为1:2.
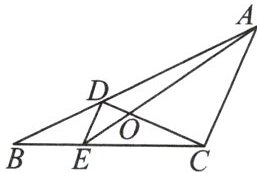
8. 如图,D、E 分别是△ABC 的边 AB、BC 上的点,且 $ DE// AC $,AE、CD 相交于点 O,若 $ S_{△DOE}:S_{△COA}= 1:9 $,则 $ S_{△BDE} $ 与 $ S_{△CDE} $ 的比是 (
A.$ 1:2 $
B.$ 1:3 $
C.$ 1:4 $
D.$ 2:5 $
A
)
A.$ 1:2 $
B.$ 1:3 $
C.$ 1:4 $
D.$ 2:5 $
答案:
A
查看更多完整答案,请扫码查看


