《2025年名校课堂内外九年级数学上册湘教版湖南专版》

10. 函数 $ y = (m - 1)x^{|m| - 2} $ 是反比例函数,则 $ m $ 的值为 -1。

答案： -1

11. 下列函数：$ xy = 1 $,$ y = \frac{x}{3} $,$ y = \frac{2m}{x} $,$ y = \frac{1}{x - 2} $,$ y = \frac{2}{x^{2}} $,$ y = \frac{3}{x} + 1 $ 中,是 $ y $ 关于 $ x $ 的反比例函数的有 (A)
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个

答案： A

12. (衡东县期末)已知函数 $ y = (k - 2)x^{k^{2} - 5} $($ k $ 为常数)是反比例函数,则 $ k $ 的值是-2。

答案： -2

13. (湖南省中考改编)已知 $ y $ 与 $ 4z $ 成反比例关系,比例系数为 $ k_{1} $,$ z $ 与 $ \frac{1}{4}x $ 成正比例关系,比例系数为 $ k_{2} $,$ k_{1} $ 和 $ k_{2} $ 是已知数,且 $ k_{1} \cdot k_{2} \neq 0 $,则 $ y $ 与 $ x $ 成 反比例关系。(填“正”或“反”)

答案： 反

14. 已知一个三角形的面积是 $ 30cm^{2} $,它的底边长是 $ a cm $,底边上的高是 $ h cm $。
(1)写出 $ h $ 与 $ a $ 之间的函数表达式；
(2)当 $ h = 6 $ 时,求 $ a $ 的值。

答案：
(1)解:$ \because \frac{1}{2}ah=30 $,$ \therefore h=\frac{60}{a} $.
(2)当$ h=6 $时,$ 6=\frac{60}{a} $,$ \therefore a=10 $.

15. (浙江省中考改编)科学课上,同学用自制密度计测量液体的密度。密度计悬浮在不同的液体中时,浸在液体中的高度 $ h $(单位：$ cm $)是液体的密度 $ \rho $(单位：$ g/cm^{3} $)的反比例函数。
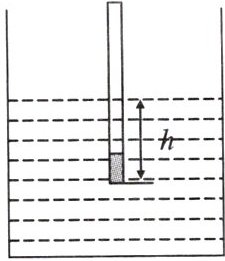
(1)当密度计悬浮在密度为 $ 1g/cm^{3} $ 的水中时,$ h = 20cm $。求 $ h $ 关于 $ \rho $ 的函数表达式；
(2)当密度计悬浮在另一种液体中时,$ h = 25cm $,求该液体的密度 $ \rho $。

答案：
(1)解:$ \because \rho \cdot h=20 $.$ \therefore h $关于$ \rho $的函数表达式为$ h=\frac{20}{\rho} $;
(2)把$ h=25 $代入$ h=\frac{20}{\rho} $,得$ 25=\frac{20}{\rho} $,解得:$ \rho=0.8 $,答:该液体的密度$ \rho $为$ 0.8g/cm^{3} $.

16. (新定义型阅读理解题)定义：形如 $ y = ax + \frac{b}{x} $($ ab ＞ 0 $)的函数称为“双飞燕函数”。已知函数 $ y = (k - 1)x - x^{k^{2} - 3} $ 是“双飞燕函数”,则 $ k $ 的值为 (B)
A.$ \sqrt{2} $
B.$ - \sqrt{2} $
C.$ 2 $
D.$ - 2 $

答案： B

17. (核心素养·几何直观)李贝说：“在如图所示的矩形 $ ABCD $ 中,$ AB = 6 $,$ BC = 8 $,$ P $ 是 $ BC $ 边上一动点,过点 $ D $ 作 $ DE \perp AP $ 于点 $ E $。设 $ AP = x $($ x \leq 10 $),$ DE = y $,则 $ y $ 是 $ x $ 的反比例函数。”你认为李贝说得对吗？请说明理由。

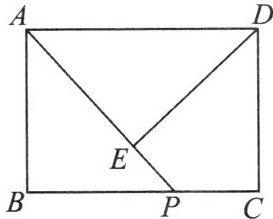
答案： 解:李贝说得对,理由如下:连接DP,$ S_{\triangle ADP}=\frac{1}{2}AD\cdot AB=\frac{1}{2}× 6× $8=24,又$ S_{\triangle APD}=\frac{1}{2}AP\cdot DE=\frac{1}{2} $xy=24,$ \therefore y=\frac{48}{x}(6\leqslant x\leqslant 10) $,$ \therefore y $是x的反比例函数.