《2025年名校课堂内外九年级数学上册湘教版湖南专版》

8. (武冈市期末)如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是 (D)

A.$\frac{ED}{EA}= \frac{DF}{AB}$
B.$\frac{DE}{CB}= \frac{EF}{FB}$
C.$\frac{BF}{BE}= \frac{BC}{AE}$
D.$\frac{BC}{DE}= \frac{BF}{BE}$

答案： D

9. 如图,在平行四边形ABCD中,F是AD上一点,且$AF= \frac{3}{2}FD$,连接BF并延长交CD的延长线于点G,则$\frac{BE}{EG}$的值为______.

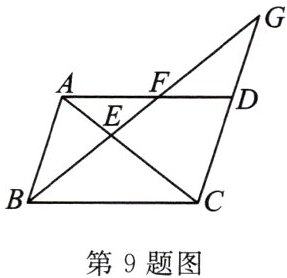
$\frac{3}{5}$

答案： $\frac{3}{5}$

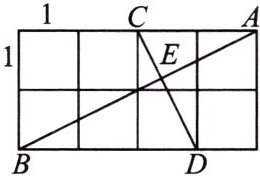
10. (新考法)如图是钉板示意图,每两个相邻的钉点长为1个单位,钉点A,B的连线与钉点C,D的连线交于点E,则AE= $\frac{4\sqrt{5}}{5}$.

答案： $\frac{4\sqrt{5}}{5}$

11. 如图,已知菱形ABCD的边长为3,延长AB到点E,使BE= 2AB,连接EC并延长交AD的延长线于点F,求AF的长.

答案： 解：
∵四边形ABCD是菱形，
∴BC//AD，即BC//AF，
∴△EAF∽△EBC，
∴$\frac{AF}{BC}$=$\frac{AE}{BE}$.
∵BC=CD=DA=AB=3，
∴BE=2AB=6.
∴AF=$\frac{BC·AE}{BE}$=$\frac{3×(3+6)}{6}$=4.5.

12. (教材第79页练习第2题变式)如图,在▱ABCD中,点F在对角线BD上,EF//AB交AD于点E,FG//ED交CD于点G,DE：DA= 2：5,EF= 4,求线段CG的长.

答案： 解：
∵EF//AB，
∴△DEF∽△DAB，
∴$\frac{EF}{AB}$=$\frac{DE}{DA}$，
∵$\frac{DE}{DA}$=$\frac{2}{5}$，EF=4，
∴$\frac{4}{AB}$=$\frac{DE}{DA}$=$\frac{2}{5}$，
∴AB=10，
∵四边形ABCD是平行四边形，
∴AB=CD，同理EF=DG，
∴CG=10-4=6.

13. (核心素养·推理能力)如图,线段CD//AB,AD与BC交于点E.
(1)求证：AE·CE= DE·BE；
(2)过点E作EF//AB,交AC于点F,如果AB= 5,EF= 2,求CD的长.

答案： （1）证明：
∵CD//AB，
∴△ABE∽△DCE，
∴$\frac{AE}{DE}$=$\frac{BE}{CE}$，
∴AE·CE=DE·BE. （2）解：
∵EF//AB，
∴△CEF∽△CBA.
∴$\frac{CF}{CA}$=$\frac{EF}{AB}$=$\frac{2}{5}$，
∴$\frac{AF}{AC}$=$\frac{3}{5}$.
∵CD//AB，EF//AB，
∴EF//CD，
∴△AEF∽△ADC，
∴$\frac{EF}{DC}$=$\frac{AF}{AC}$，
∴$\frac{2}{CD}$=$\frac{3}{5}$，即CD=$\frac{10}{3}$.