《2025年名校课堂内外九年级数学上册湘教版湖南专版》

7. (岳阳岳州中学单元卷)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强 $ p(Pa) $ 是气球体积 $ V(m^{3}) $ 的反比例函数,且当 $ V = 3m^{3} $ 时,$ p = 8000Pa $. 当气球内的气体压强大于 $ 40000Pa $ 时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于0.6 $ m^{3} $.

答案： 0.6

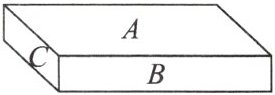
8. 如图,一块砖的 $ A $,$ B $,$ C $ 三个面的面积之比是 $ 5:3:1 $. 如果 $ A $,$ B $,$ C $ 三个面分别放在地上,地面所受压强分别为 $ p_{1} $,$ p_{2} $,$ p_{3} $,压强的计算公式为 $ p= \frac{F}{S} $,其中 $ p $ 是压强,$ F $ 是压力,$ S $ 是受力面积,则 $ p_{1} $,$ p_{2} $,$ p_{3} $ 的大小关系为$ p_{1}＜p_{2}＜p_{3} $(用“$＜$”连接).

答案： $ p_{1}＜p_{2}＜p_{3} $

9. (宁夏自治区中考)给某气球充满一定质量的气体,在温度不变时,气球内气体的气压 $ p(KPa) $ 是气体体积 $ V(m^{3}) $ 的反比例函数,其图象如图所示.
(1)当气球内的气压超过 $ 150KPa $ 时,气球会爆炸,若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 $ V= \frac{4}{3}\pi r^{3} $,$ \pi $ 取 3)；
(2)请你利用 $ p $ 与 $ V $ 的关系试解释为什么超载的车辆容易爆胎.

答案：
(1)解:设函数关系式为$ p=\frac{k}{V} $,根据图象可得:$ k=pV=120×0.04=4.8 $,
∴$ p=\frac{4.8}{V} $,
∴当$ p=150 $时,$ V=\frac{4.8}{150}=0.032 $,
∴$ \frac{4}{3}×3r^{3}=0.032 $,解得:$ r=0.2 $,
∵$ k=4.8＞0 $,
∴p随V的增大而减小,
∴要使气球不会爆炸,$ V\geq0.032 $,此时$ r\geq0.2 $,
∴气球的半径至少为0.2m时,气球不会爆炸;
(2)由于车辆超载,轮胎体积变小,胎内气压增大导致爆胎.

10. (核心素养·应用意识)根据传染病防控制度的要求,学校必须对教室定期用药熏消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量 $ y $(毫克)与时间 $ x $(分钟)成正比例；药物燃烧完毕后,$ y $(毫克)与时间 $ x $(分钟)成反比例,如图所示. 请根据图中所提供的信息,解答下列问题：
(1)当药物燃烧时,$ y $ 关于 $ x $ 的函数关系式为$ y=2x $,自变量 $ x $ 的取值范围为$ 0\leq x\leq4 $；药物燃烧完毕后,$ y $ 关于 $ x $ 的函数关系式为$ y=\frac{32}{x} $；
(2)研究表明,当空气中每立方米的含药量低于 1.6 毫克时学生方可进入教室,则从消毒开始,至少需要经过20分钟后,学生才能回到教室；
(3)研究表明,当空气中每立方米的含药量不低于 2 毫克且持续时间不低于 14 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效？为什么？
解:此次消毒有效,理由:当$ y=2 $时,$ y=\frac{32}{x}=2 $,解得$ x=16 $,当$ y=2 $时,$ y=2x=2 $,解得$ x=1 $,
∵$ 16-1=15＞14 $,
∴此次消毒有效.

答案：
(1)$ y=2x $ $ 0\leq x\leq4 $ $ y=\frac{32}{x} $
(2)20
(3)解:此次消毒有效,理由:当$ y=2 $时,$ y=\frac{32}{x}=2 $,解得$ x=16 $,当$ y=2 $时,$ y=2x=2 $,解得$ x=1 $,
∵$ 16-1=15＞14 $,
∴此次消毒有效.