第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
5. 【新知理解】如图(1),若点A,B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.
作法:作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
【解决问题】如图(2),AD是等边三角形ABC的中线,AD= 6 cm,点P,E分别为AD,AC上的动点,则PC+PE的最小值为______ cm.
【拓展研究】如图(3),在四边形ABCD的对角线AC上找一点P,使∠APB= ∠APD.(保留作图痕迹,并对作图方法进行说明)
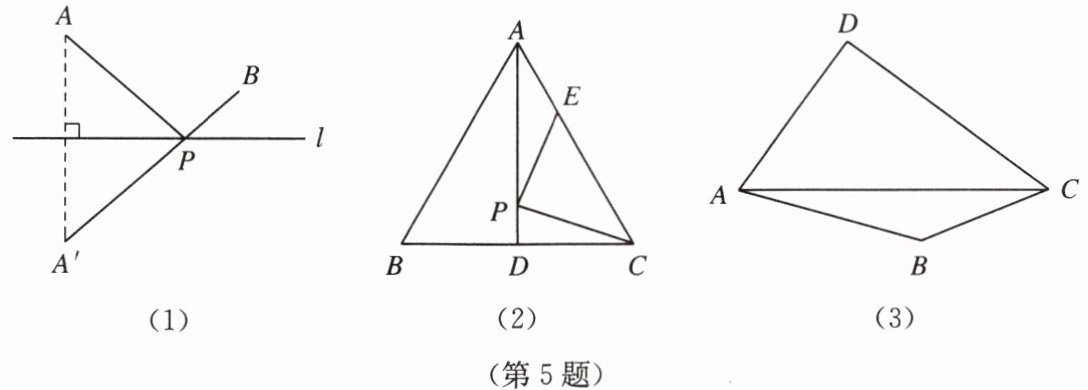
作法:作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
【解决问题】如图(2),AD是等边三角形ABC的中线,AD= 6 cm,点P,E分别为AD,AC上的动点,则PC+PE的最小值为______ cm.
【拓展研究】如图(3),在四边形ABCD的对角线AC上找一点P,使∠APB= ∠APD.(保留作图痕迹,并对作图方法进行说明)

答案:
[解决问题]如图
(1),作点 E 关于AD的对称点 F,连接 PF,则 PE=PF. 当点 F,P,C 在一条直线上时,PC+PE=PC+PF=CF(最短),当 CF⊥AB 时,CF 最短,CF=AD=6 cm. (2)[拓展研究]方法1:如图
(2),作点 B 关于 AC 的对称点 E,连接 DE 并延长,交 AC 于点 P,点 P 即为所求,连接 BP,则∠APB=∠APD. 方法2:作点 D 关于 AC 的对称点 D',连接 D'B 并延长与 AC 交于点 P,点 P 即为所求,连接 DP,则∠APB=∠APD.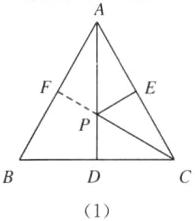
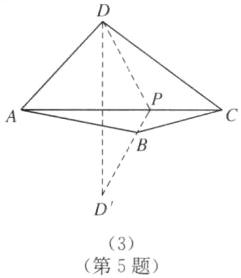
[解决问题]如图
(1),作点 E 关于AD的对称点 F,连接 PF,则 PE=PF. 当点 F,P,C 在一条直线上时,PC+PE=PC+PF=CF(最短),当 CF⊥AB 时,CF 最短,CF=AD=6 cm. (2)[拓展研究]方法1:如图
(2),作点 B 关于 AC 的对称点 E,连接 DE 并延长,交 AC 于点 P,点 P 即为所求,连接 BP,则∠APB=∠APD. 方法2:作点 D 关于 AC 的对称点 D',连接 D'B 并延长与 AC 交于点 P,点 P 即为所求,连接 DP,则∠APB=∠APD.


如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使所有黑色部分的图形仍然构成一个轴对称图形,则符合条件的白色小正方形的个数有______个.


答案:
提示:如图所示,有5个.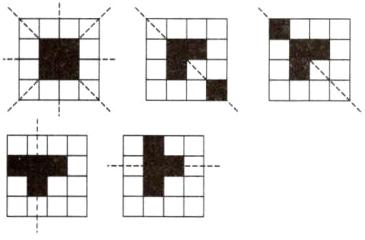
提示:如图所示,有5个.

1. 已知点A(-3,-4)平移后能与原来的位置关于y轴对称,则应把点A(
A.向左平移6个单位长度
B.向右平移6个单位长度
C.向下平移8个单位长度
D.向上平移8个单位长度
B
)A.向左平移6个单位长度
B.向右平移6个单位长度
C.向下平移8个单位长度
D.向上平移8个单位长度
答案:
B.
2. 在平面直角坐标系中,点P(-2,3)关于y轴对称的点的坐标为
(2,3)
.
答案:
(2,3)
3. 点A(-2,-1)与点B(2,-1)关于
y
轴对称.
答案:
y.
问题(1)利用平面直角坐标系,分别写出点(2,2),(-2,3),(4,-1)关于直线x= 1对称的点的坐标;
(2)分别写出(1)中各点关于直线x= -1对称的点的坐标;
(3)写出点(a,b)关于直线x= m对称的点的坐标.
名师指导
问题(1)(2)可先在平面直角坐标系中画出已知点和它们的对称点,再写出坐标.
问题(3)可观察和分析(1)(2)中各对对称点坐标之间的关系,总结、归纳出规律.
解题示范(学生在教师指导下,独立完成)
解:
(2)分别写出(1)中各点关于直线x= -1对称的点的坐标;
(3)写出点(a,b)关于直线x= m对称的点的坐标.
名师指导
问题(1)(2)可先在平面直角坐标系中画出已知点和它们的对称点,再写出坐标.
问题(3)可观察和分析(1)(2)中各对对称点坐标之间的关系,总结、归纳出规律.
解题示范(学生在教师指导下,独立完成)
解:
答案:
(1) 点(2,2)关于直线x=1对称的点:横坐标为2×1 - 2=0,坐标(0,2);
点(-2,3)关于直线x=1对称的点:横坐标为2×1 - (-2)=4,坐标(4,3);
点(4,-1)关于直线x=1对称的点:横坐标为2×1 - 4=-2,坐标(-2,-1)。
(2) 点(2,2)关于直线x=-1对称的点:横坐标为2×(-1) - 2=-4,坐标(-4,2);
点(-2,3)关于直线x=-1对称的点:横坐标为2×(-1) - (-2)=0,坐标(0,3);
点(4,-1)关于直线x=-1对称的点:横坐标为2×(-1) - 4=-6,坐标(-6,-1)。
(3) 点(a,b)关于直线x=m对称的点的坐标为(2m - a, b)。
(1) 点(2,2)关于直线x=1对称的点:横坐标为2×1 - 2=0,坐标(0,2);
点(-2,3)关于直线x=1对称的点:横坐标为2×1 - (-2)=4,坐标(4,3);
点(4,-1)关于直线x=1对称的点:横坐标为2×1 - 4=-2,坐标(-2,-1)。
(2) 点(2,2)关于直线x=-1对称的点:横坐标为2×(-1) - 2=-4,坐标(-4,2);
点(-2,3)关于直线x=-1对称的点:横坐标为2×(-1) - (-2)=0,坐标(0,3);
点(4,-1)关于直线x=-1对称的点:横坐标为2×(-1) - 4=-6,坐标(-6,-1)。
(3) 点(a,b)关于直线x=m对称的点的坐标为(2m - a, b)。
查看更多完整答案,请扫码查看


