《2025年新课程自主学习与测评八年级数学上册人教版》

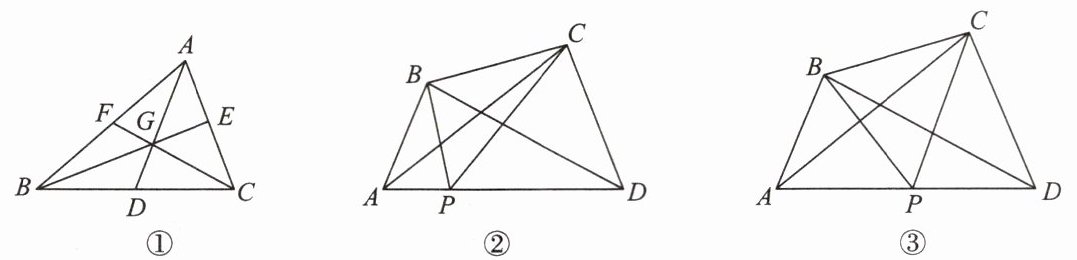
【操作发现】三角形三个顶点与重心的连线段,将该三角形面积三等分.
(1)如图①,在△ABC中,中线AD,BE,CF相交于点G. 求证：S₍△ABG₎= 1/3 S₍△ABC₎.
【提出问题】如图②,探究在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间的关系.
(2)为了解决这个问题,我们可以先从一些简单的、特殊的情形入手：如图③,当AP= 1/2 AD时,探求S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系,写出求解过程.

【问题解决】
(3)推广,当AP= 1/n AD(n表示正整数)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系：$S_{\triangle PBC}=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$.
(4)一般地,当AP= m/n AD(0≤m/n ≤1)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系：$S_{\triangle PBC}=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$.
(1)如题图①，$\because BD=CD$，$\therefore S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$. $\because G$是重心，$\therefore AG=2DG$，$\therefore S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$.
(2)结论：$S_{\triangle PBC}=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$. 理由：如题图③，$\because AP=\frac{1}{2}AD$，$\triangle ABP$和$\triangle ABD$的高相等，$\therefore S_{\triangle ABP}=\frac{1}{2}S_{\triangle ABD}$. $\because PD=\frac{1}{2}AD$，$\triangle CDP$和$\triangle CDA$的高相等，$\therefore S_{\triangle CDP}=\frac{1}{2}S_{\triangle CDA}$. $\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{2}S_{\triangle ABD}-\frac{1}{2}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$.

答案：
(1) 如题图①，$\because BD=CD$，$\therefore S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$. $\because G$是重心，$\therefore AG=2DG$，$\therefore S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$.
(2) 结论：$S_{\triangle PBC}=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$. 理由：如题图③，$\because AP=\frac{1}{2}AD$，$\triangle ABP$和$\triangle ABD$的高相等，$\therefore S_{\triangle ABP}=\frac{1}{2}S_{\triangle ABD}$. $\because PD=\frac{1}{2}AD$，$\triangle CDP$和$\triangle CDA$的高相等，$\therefore S_{\triangle CDP}=\frac{1}{2}S_{\triangle CDA}$. $\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{2}S_{\triangle ABD}-\frac{1}{2}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$.
(3) 结论：$S_{\triangle PBC}=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$. 理由：$\because AP=\frac{1}{n}AD$，$\triangle ABP$和$\triangle ABD$的高相等，$\therefore S_{\triangle ABP}=\frac{1}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - 1}{n}AD$，$\triangle CDP$和$\triangle CDA$的高相等，$\therefore S_{\triangle CDP}=\frac{n - 1}{n}S_{\triangle CDA}$，$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{n}S_{\triangle ABD}-\frac{n - 1}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - 1}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$.
(4) 结论：$S_{\triangle PBC}=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$. 理由：$\because AP=\frac{m}{n}AD$，$\triangle ABP$和$\triangle ABD$的高相等，$\therefore S_{\triangle ABP}=\frac{m}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - m}{n}AD$，$\triangle CDP$和$\triangle CDA$的高相等，$\therefore S_{\triangle CDP}=\frac{n - m}{n}S_{\triangle CDA}$，$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{m}{n}S_{\triangle ABD}-\frac{n - m}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{m}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - m}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$.