《2025年资源与评价黑龙江教育出版社九年级数学上册人教版》

1. 如图,如果$AB为\odot O$的直径,弦$CD\perp AB$,垂足为$E$,那么下列结论中,错误的是(D)

A.$CE = DE$
B.$\overset{\frown}{BC}= \overset{\frown}{BD}$
C.$\angle BAC= \angle BAD$
D.$AC＞AD$

答案： D

2. 下列命题中,不正确的是(C)
A.垂直于弦的直径平分这条弦
B.平分弦(不是直径)的直径垂直于这条弦
C.弦的垂直平分线是圆的直径
D.平分弦所对的一条弧的直径垂直这条弦

答案： C

3. 如图,$\odot O的直径为10$,圆心$O到弦AB的距离OM的长为3$,则弦$AB$的长是(D)

A.$4$
B.$6$
C.$7$
D.$8$

答案： D

4. 两个圆心相同、半径不等的圆的对称轴有无数条。

答案： 无数

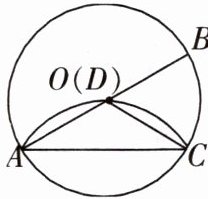
5. 如图,在$\odot O$中,$AB$为直径,$C$为圆上一点,将劣弧沿弦$AC翻折交AB于点D$,连接$CD$,若点$D与圆心O$重合,$AC = 2$,求$\odot O的半径r$。

答案： 解:如图，过圆心O作OF⊥AC于点F，延长OF交⊙O于点E.
∵AC=2,
∴AF=FC=1.在Rt△OFC中，
∵OF=EF=$\frac{1}{2}$r,OC=r,
∴由勾股定理得$1^2+(\frac{1}{2}r)^2=r^2$,
∴r=$\frac{2\sqrt{3}}{3}$,即⊙O的半径r为$\frac{2\sqrt{3}}{3}$.

6. 如图1,筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理。如图2,筒车盛水桶的运行轨道是以轴心$O$为圆心的圆。已知圆心$O$在水面上方,且$\odot O被水面截得的弦AB的长为6$米,$\odot O的半径长为4$米。若点$C$为运行轨道的最低点,则点$C到弦AB$所在直线的距离是(A)

A.$(4 - \sqrt{7})$米
B.$2$米
C.$3$米
D.$(4 + \sqrt{7})$米

答案： A

7. $\odot O的直径为10$,弦$AB的长为8$,$P是弦AB$上的一个动点,则$OP$的取值范围是3≤OP≤5。

答案： 3≤OP≤5

8. 如图,某地有一座圆弧形的拱桥,桥下水面宽为$12$米,拱顶高出水面$4$米。
(1)求这座拱桥所在圆的半径。
(2)现有一艘宽$5$米,船舱顶部为正方形并高出水面$3.6$米的货船要经过这里,此时货船能顺利通过这座拱桥吗？请说明理由。

答案： 解:
(1)如图，连接OA.根据题意得CD=4米,AB=12米,AD=$\frac{1}{2}$AB=6(米).设这座拱桥所在圆的半径为x米，则OA=OC=x米,OD=OC−CD=(x - 4)米，在Rt△AOD中,OA²=OD²+AD²,则$x^2=(x - 4)^2+6^2$,解得x=6.5米.故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:连接OM,设MN=5米，
∵OC⊥MN,
∴MH=$\frac{1}{2}$MN=2.5(米).在Rt△OMH中,OH=$\sqrt{OM^2 - MH^2}$=6(米)，
∵OD=OC−CD=6.5−4=2.5(米),ME=OH - OD=6−2.5=3.5(米)＜3.6(米)，
∴货船不能顺利通过这座拱桥.