第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,在 $ \odot O $ 中,点 $ A $, $ O $, $ D $ 以及点 $ B $, $ O $, $ C $ 分别在一条直线上,则图中的弦有(
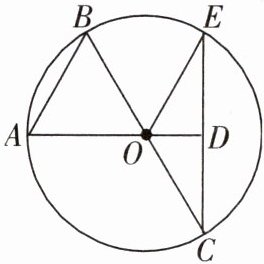
A.2 条
B.3 条
C.4 条
D.5 条
B
)
A.2 条
B.3 条
C.4 条
D.5 条
答案:
B
2. 东汉初年,我国的《周髀算经》里就有“径一周三”的古率,提出了圆的直径与周长之间存在一定的比例关系。将图中的半圆弧形铁丝 $ \overset{\frown}{MN} $ 向右水平拉直(保持 $ M $ 端不动),根据该古率,与拉直后铁丝 $ N $ 端的位置最接近的是(

A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
A
)
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
答案:
A
1. 过圆上一点可以作圆的最长弦的条数为(
A.1
B.2
C.3
D.无数条
A
)A.1
B.2
C.3
D.无数条
答案:
A
2. 等于 $ \dfrac{1}{3} $ 圆周的弧是(
A.劣弧
B.半圆
C.优弧
D.圆
A
)A.劣弧
B.半圆
C.优弧
D.圆
答案:
A
3. 到定点 $ O $ 的距离为 5 的点的集合是以
点O
为圆心,5
为半径的圆。
答案:
点O 5
4. 如图,在 $ \odot O $ 中,点 $ A $, $ O $, $ D $,点 $ B $, $ O $, $ C $ 分别在一直线上,图中弦的条数为

两条
。
答案:
两条
5. 已知 $ \odot O $ 的半径为 2,弦 $ AB $ 的长为 $ 2\sqrt{2} $,则 $ \angle AOB $ 的度数为(
A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
D
)A.$ 30^{\circ} $
B.$ 45^{\circ} $
C.$ 60^{\circ} $
D.$ 90^{\circ} $
答案:
D
6. 在 $ \odot O $ 中,若弦 $ AB $ 等于 $ \odot O $ 的半径,则 $ \triangle AOB $ 的形状是
等边三角形
。
答案:
等边三角形
7. 如图,在 $ \odot O $ 中,若 $ \angle A = 40^{\circ} $,则 $ \angle ABO = $

40°
, $ \angle C = $50°
, $ \angle ABC = $90°
。
答案:
40° 50° 90°
8. $ \odot O $ 的半径为 2, $ A $ 为 $ \odot O $ 上一定点, $ P $ 在 $ \odot O $ 上沿圆周运动(不与 $ A $ 点重合),则弦 $ AP $ 的长度为整数的弦共有
7
条。
答案:
7 提示:如图.
∵⊙O的直径AB=4,
∴弦长的整数值有1,2,3,4 四种可能,
这样的弦共有7条.
故答案为7.
∵⊙O的直径AB=4,
∴弦长的整数值有1,2,3,4 四种可能,
这样的弦共有7条.
故答案为7.
9. 如图, $ BD $, $ CE $ 是 $ \triangle ABC $ 的高,求证: $ E $, $ B $, $ C $, $ D $ 四点在同一个圆上。


答案:
证明:如图,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形,
∴DF,EF分别为Rt△BCD,Rt△BCE斜边上的中线,
∴DF=EF=BF=CF,
∴E,B,C,D四点在以点F为圆心,$\frac{1}{2}$BC的长为半径的圆上.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形,
∴DF,EF分别为Rt△BCD,Rt△BCE斜边上的中线,
∴DF=EF=BF=CF,
∴E,B,C,D四点在以点F为圆心,$\frac{1}{2}$BC的长为半径的圆上.
查看更多完整答案,请扫码查看


