第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
如图,在平面直角坐标系中,将点P(2,3)绕原点O旋转90°得到点P',则点P'的坐标为

(3,-2)或(-3,2)
。
答案:
(3,-2)或(-3,2)
1. 下面的图案不能由一个图形通过旋转而构成的是(

B
)
答案:
B
2. 如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC= 2。将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是(

A.(-1,2)
B.(-4,2)
C.(3,2)
D.(2,2)
D
)
A.(-1,2)
B.(-4,2)
C.(3,2)
D.(2,2)
答案:
D
3. 如图,将正三角形OAB绕点O依次逆时针旋转五次,构成的图形是(
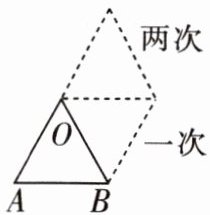
A.正六边形
B.正方形
C.正八边形
D.正五边形
A
)
A.正六边形
B.正方形
C.正八边形
D.正五边形
答案:
A
4. 如图,在网格中有一个四边形图案。
(1)请你画出此图案绕点O按顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错。
(2)若网格中每个小正方形的边长均为1,旋转后点A的对应点依次为$A_1,A_2,A_3,$求四边形$AA_1A_2A_3$的面积。
(3)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论。

(1)请你画出此图案绕点O按顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错。
(2)若网格中每个小正方形的边长均为1,旋转后点A的对应点依次为$A_1,A_2,A_3,$求四边形$AA_1A_2A_3$的面积。
(3)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论。

答案:
解:
(1)如图.
(2)如图,$S_{四边形AA_{1}A_{2}A_{3}}=S_{四边形BB_{1}B_{2}B_{3}}-4S_{\triangle BAA_{3}}=(3+5)^{2}-4×\frac{1}{2}×3×5=34.$故四边形$AA_{1}A_{2}A_{3}$的面积为34.
(3)结论:勾股定理.
解:
(1)如图.
(2)如图,$S_{四边形AA_{1}A_{2}A_{3}}=S_{四边形BB_{1}B_{2}B_{3}}-4S_{\triangle BAA_{3}}=(3+5)^{2}-4×\frac{1}{2}×3×5=34.$故四边形$AA_{1}A_{2}A_{3}$的面积为34.
(3)结论:勾股定理.

查看更多完整答案,请扫码查看


