《2025年高分突破课时达标讲练测七年级数学上册北师大版》

1. 下面的平面图形中是扇形的是( )

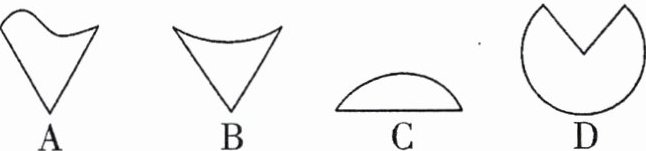
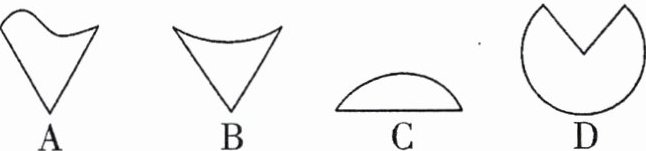
A.
B.
C.
D.

答案： D

2. 从六边形的一个顶点出发,可连出的对角线条数为( )

A.3
B.4
C.5
D.6

答案： A

3.【教材改编】如图,把一个圆分成三个扇形,则∠AOB的度数为( )


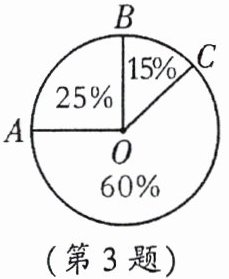
A.36°
B.54°
C.90°
D.216°

答案： C

4. 下列说法正确的有( )
①把一个角分成两个角的射线叫作这个角的角平分线；
②连接C,D两点的线段叫两点之间的距离；
③两点之间直线最短；
④射线上点的个数是直线上点的个数的一半；
⑤n边形从其中一个顶点出发连接其余各顶点,可以画出(n-3)条对角线,这些对角线把这个n边形分成了(n-2)个三角形。

A.3个
B.2个
C.1个
D.0个

答案： C

5. 过多边形的一个顶点可以作2025条对角线,则这个多边形的边数是______。

答案： 2028

6. 如图,一根6m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是$______m^2。$
]

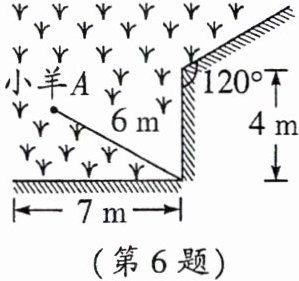
答案： $\frac{29}{3}\pi$

7. 将一个半径为2的圆分割成四个扇形,它们的圆心角度数之比为1:3:2:4,请你求出这四个扇形的圆心角的度数以及这四个扇形的面积。

答案： $36^\circ, 108^\circ, 72^\circ,$ $144^\circ$; $\frac{2\pi}{5},\frac{6\pi}{5},\frac{4\pi}{5},\frac{8\pi}{5}$

8. 下列说法：①由许多条线段连接而成的图形叫作多边形；②在同一个圆中,两端点都在圆上的线段中,最长的是直径；③角的边越长,角越大；④一条射线就是一个周角。其中正确的结论有( )

A.1个
B.2个
C.3个
D.0个

答案： A

9. (1)从一个十边形的某条边上一点出发,分别连接这个点与各顶点,可以把十边形分割成______个三角形；
(2)已知从九边形的一个顶点出发,可引出m条对角线,这些对角线可以把这个九边形分成n个三角形,则m-n= ______。

答案：
(1)9
(2)-1

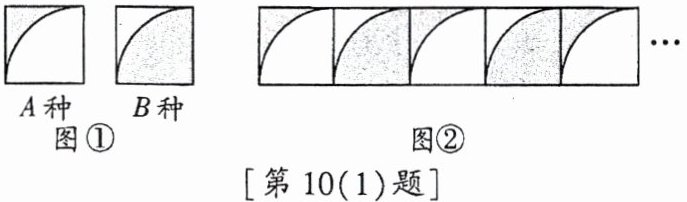
10. (1)边长为2的两种正方形卡片如图①所示,卡片中的扇形半径均为2。图②是交替摆放A,B两种卡片得到的图案。若摆放这个图案共用两种卡片21张,则这个图案中阴影部分的面积和为______；(结果保留π)

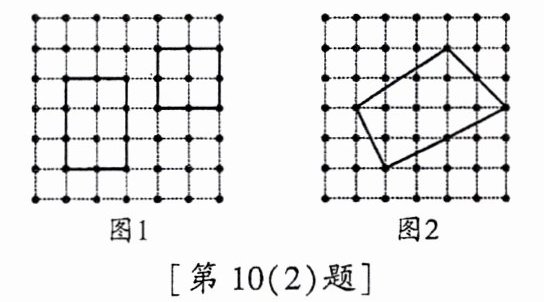
(2)“皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为$S= a+\frac{b}{2}-1$。小明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图1探究,并运用探究的结果求出图2中多边形的面积是______。
]

答案：
(1)$44-\pi$
(2)10