第5页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
11. 如图所示,由 27 个完全相同的小方块堆成一个正方体,如果将它的表面涂成黄色。
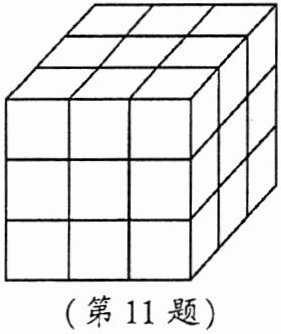
(1)有 3 个面涂成黄色的小方块有几块?
(2)有 1 个面涂成黄色的小方块有几块?
(3)有 2 个面涂成黄色的小方块有几块?

(1)有 3 个面涂成黄色的小方块有几块?
(2)有 1 个面涂成黄色的小方块有几块?
(3)有 2 个面涂成黄色的小方块有几块?
答案:
(1)4 8
(2)6 块 12 12 块 12 20 12 30 V+F-E=2
(2)20
(3)14
(1)4 8
(2)6 块 12 12 块 12 20 12 30 V+F-E=2
(2)20
(3)14
12. (1)有两个完全相同的长方体,长、宽、高分别是 5 cm,4 cm,3 cm,把它们叠放在一起组成一个新的长方体,在这些新的长方体的表面积中,最大的是$______cm^2;$
(2)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 90°算一次,则滚动第 3 次后,骰子朝下一面的点数是______。(填数字)
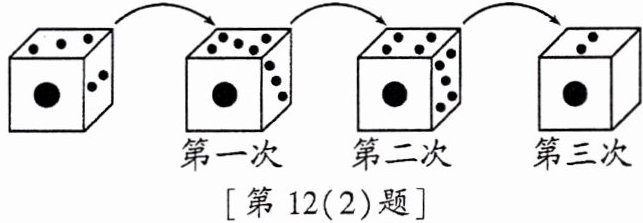
(2)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动 90°算一次,则滚动第 3 次后,骰子朝下一面的点数是______。(填数字)

答案:
(1)20
(2)12
(1)20
(2)12
13. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在一个有趣的关系式,被称为欧拉公式。请你观察下列几种简单多面体模型,解答下列问题:
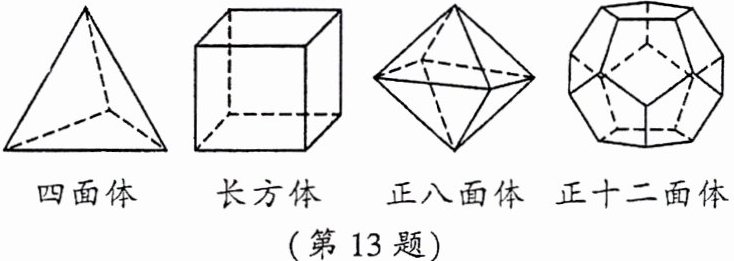
(1)根据上列多面体模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | | | |
| 长方体 | | | |
| 正八面体 | | | |
| 正十二面体 | | | |
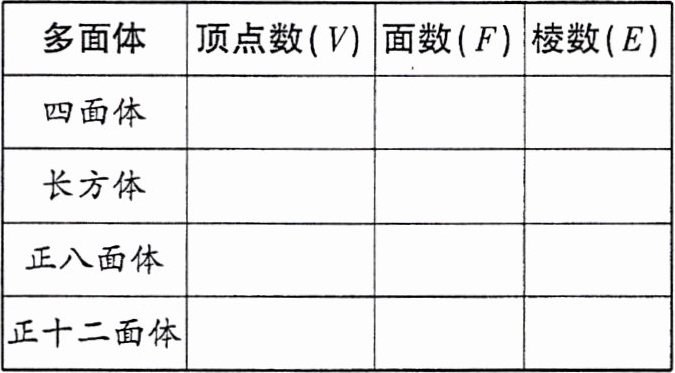
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是______;
(2)一个多面体的面数比顶点数大 8,且有 30 条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有 24 个顶点,每个顶点处都有 3 条棱。求该多面体的面数 F。

(1)根据上列多面体模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | | | |
| 长方体 | | | |
| 正八面体 | | | |
| 正十二面体 | | | |

你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是______;
(2)一个多面体的面数比顶点数大 8,且有 30 条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有 24 个顶点,每个顶点处都有 3 条棱。求该多面体的面数 F。
答案:
(1) V+F-E=2
(2)20
(3)14
(1) V+F-E=2
(2)20
(3)14
查看更多完整答案,请扫码查看


