第72页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 按一定规律排列的多项式:$a+b$,$a^{3}+b^{2}$,$a^{5}+b^{3}$,$a^{7}+b^{4}$,$a^{9}+b^{5}$,…,第$n$个多项式是 ( )
A.$a^{2n-1}+b^{n}$
B.$a^{2n+1}+b^{n}$
C.$a^{2n-1}+b^{n+1}$
D.$a^{2n+1}+b^{n+1}$
A.$a^{2n-1}+b^{n}$
B.$a^{2n+1}+b^{n}$
C.$a^{2n-1}+b^{n+1}$
D.$a^{2n+1}+b^{n+1}$
答案:
A
2. 【跨学科融合】“数学是将科学现象升华到科学本质认识的重要工具”。比如化学中,甲醇的化学式为$CH_3OH$,乙醇的化学式为$C_2H_5OH$,丙醇的化学式为$C_3H_7OH$……可以预见醇类物质的化学式中,$C与H$的数目满足一定的数学规律,则$C$的数目为15的醇的化学式是( )
A.$C_{15}H_{30}OH$
B.$C_{15}H_{31}OH$
C.$C_{15}H_{32}OH$
D.$C_{15}H_{33}OH$
A.$C_{15}H_{30}OH$
B.$C_{15}H_{31}OH$
C.$C_{15}H_{32}OH$
D.$C_{15}H_{33}OH$
答案:
B
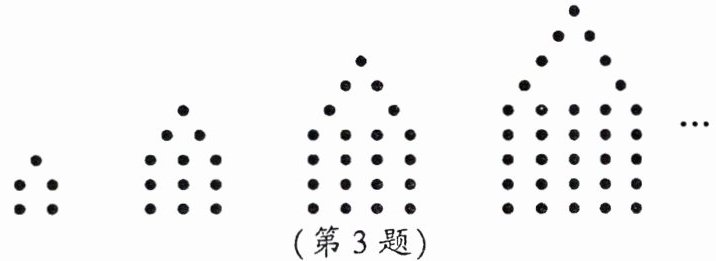
3. 某同学用大小相同的黑色棋子摆成如图所示的图形,第一个图形由5颗棋子组成,第二个图形由12颗棋子组成,第三个图形由21颗棋子组成……观察图形的变化规律,则第八个图形用的棋子数量是 ( )
A.78
B.96
C.105
D.108

A.78
B.96
C.105
D.108
答案:
B
4. 如图为一个三角形点阵,从上向下数有无数行,其中第一行有一个点,第二行有两个点,…,第$n行有n$个点,我们将前$n行的点数和记为S_n$,如$S_1= 1$,$S_4= 10$,则$S_n$不可能是 ( )

A.20
B.15
C.28
D.36

A.20
B.15
C.28
D.36
答案:
A
5. 如图,在$2×2$的网格内各有4个数字,各网格内数字都有相同的规律,根据此规律,$c$为______。
]

]

答案:
9
6. 观察$3^1+1= 4$,$3^2+1= 10$,$3^3+1= 28$,$3^4+1= 82$,$3^5+1= 244$,…,归纳各计算结果中的个位数字的规律,猜测$3^{2025}+1$的个位数字是______。
答案:
4
7. 从2开始,连续的偶数相加,它们和的情况如下表:
|加数的个数$n$| $S$ |
| 1 | $2= 1×2$ |
| 2 | $2+4= 2×3$ |
| 3 | $2+4+6= 3×4$ |
| 4 | $2+4+6+8= 4×5$ |
| 5 | $2+4+6+8+10= 5×6$ |
| ... | ... |

(1)若$n= 8$时,则$S$的值为______;
(2)根据表中的规律猜想,用含$n的式子表示S为S= 2+4+6+8+…+2n= $______;
(3)根据(2)中的规律计算:$2+4+6+…+200+202$的值。
|加数的个数$n$| $S$ |
| 1 | $2= 1×2$ |
| 2 | $2+4= 2×3$ |
| 3 | $2+4+6= 3×4$ |
| 4 | $2+4+6+8= 4×5$ |
| 5 | $2+4+6+8+10= 5×6$ |
| ... | ... |

(1)若$n= 8$时,则$S$的值为______;
(2)根据表中的规律猜想,用含$n的式子表示S为S= 2+4+6+8+…+2n= $______;
(3)根据(2)中的规律计算:$2+4+6+…+200+202$的值。
答案:
(1)72
(2)n(n+1)
(3)10 302
(1)72
(2)n(n+1)
(3)10 302
8. 【教材改编】在三角形$ABC中有一点P_1$,当点$P_1,A,B,C$没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图)。当三角形$ABC$内的点的个数增加时,若其他条件不变,三角形内互不重叠的小三角形的个数情况是怎样?

|三角形$ABC$内点的个数|1|2|3|…|1012|
|构成不重叠的小三角形的个数|3|5|7|…|?|

观察上述图形,结合上表,则表中的“?”处应是 ( )
A.2022
B.2023
C.2024
D.2025

|三角形$ABC$内点的个数|1|2|3|…|1012|
|构成不重叠的小三角形的个数|3|5|7|…|?|

观察上述图形,结合上表,则表中的“?”处应是 ( )
A.2022
B.2023
C.2024
D.2025
答案:
D
查看更多完整答案,请扫码查看


