第78页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
18. 小方家住房户型呈长方形,平面图如下(单位:m)。现准备铺设地面,三间卧室铺设木地板,其他区域铺设地砖。
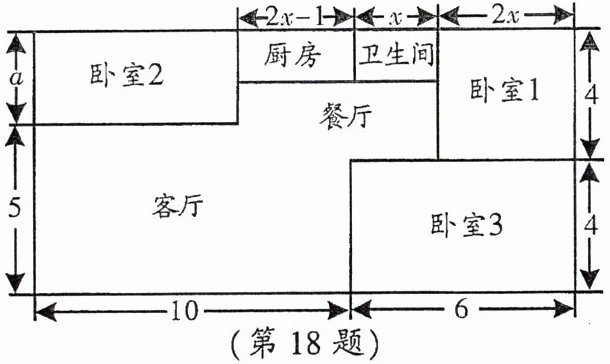
(1)求$a$的值;
(2)铺设地面需要木地板和地砖各多少平方米?(用含$x$的代数式表示)
(3)按市场价格,木地板单价为300元/$m^2$,地砖单价为100元/$m^2$。装修公司有A,B两种活动方案,如表:
|活动方案|木地板价格|地砖价格|总安装费|
|----|----|----|----|
|A|8折|8.5折|2000元|
|B|9折|8.5折|免收|
已知卧室2的面积为21 $m^2$,则小方家应选择哪种活动方案,使铺设地面总费用(含材料费及安装费)更低?

(1)求$a$的值;
(2)铺设地面需要木地板和地砖各多少平方米?(用含$x$的代数式表示)
(3)按市场价格,木地板单价为300元/$m^2$,地砖单价为100元/$m^2$。装修公司有A,B两种活动方案,如表:
|活动方案|木地板价格|地砖价格|总安装费|
|----|----|----|----|
|A|8折|8.5折|2000元|
|B|9折|8.5折|免收|
已知卧室2的面积为21 $m^2$,则小方家应选择哪种活动方案,使铺设地面总费用(含材料费及安装费)更低?
答案:
(1) 3
(2) 铺设地面需要木地板 $(75-7x)\ m^{2}$, 铺设地面需要地砖 $(7x+53)\ m^{2}$
(3) B 种活动方案
(1) 3
(2) 铺设地面需要木地板 $(75-7x)\ m^{2}$, 铺设地面需要地砖 $(7x+53)\ m^{2}$
(3) B 种活动方案
19. 有依次排列的2个整式:$x,x + 2$,对任意相邻的两个整式,都用右边的整式减去左边的整式,所得之差写在这两个整式之间,可以产生一个新整式串:$x,2,x + 2$,这称为第一次操作;将第一次操作后的整式串按上述方式再做一次操作,可以得到第二次操作后的整式串,以此类推。通过实际操作,下列结论正确的有 ( )
①第二次操作后整式串为$x,2 - x,2,x,x + 2$;
②第三次操作后整式串中的第四个整式是$x$;
③第三次操作后整式串中共有8个整式;
④第2025次操作后,所有的整式的和为$2x + 4050$。
A.1个
B.2个
C.3个
D.4个
①第二次操作后整式串为$x,2 - x,2,x,x + 2$;
②第三次操作后整式串中的第四个整式是$x$;
③第三次操作后整式串中共有8个整式;
④第2025次操作后,所有的整式的和为$2x + 4050$。
A.1个
B.2个
C.3个
D.4个
答案:
B
20. 如果一个四位自然数$\overline{abcd}$的各数位上的数字互不相等且均不为0,满足$\overline{ab}-\overline{bc}=\overline{cd}$,那么称这个四位数为“递减数”。例如:四位数4129,因为$41 - 12=29$,所以4129是“递减数”;又如:四位数5324,因为$53 - 32=21≠24$,所以5324不是“递减数”。若一个“递减数”为$\overline{a312}$,则这个数为______;若一个“递减数”的前三个数字组成的三位数$\overline{abc}$与后三个数字组成的三位数$\overline{bcd}$的和能被9整除,则满足条件的数的最大值是______。
答案:
4 312 8 165
查看更多完整答案,请扫码查看


