《2025年高分突破课时达标讲练测七年级数学上册北师大版》

9.(2025·重庆外语校)毕达哥拉斯学派常把沙滩上的沙粒或小石子用数表示，并由它们排列而成的形状对自然数进行研究。如图，第1个图形中有1个圆点，第2个图形中有6个圆点，第3个图形中有15个圆点，第4个图形中有28个圆点，…，以此类推，第6个图形对应的圆点数为（ ）

A.45
B.66
C.65
D.91

答案： B

10.意大利著名数学家斐波那契发现有这样一组数：1,1,2,3,5,8,13,…，其中从第三个数起，每一个数都等于它前面两个数的和。现以这组数中的各个数作为正方形的边长值分别构造正方形，再从左到右分别取前2个、前3个、前4个、前5个正方形拼成如图所示的若干个长方形，并按序依次记为①,②,③,④,…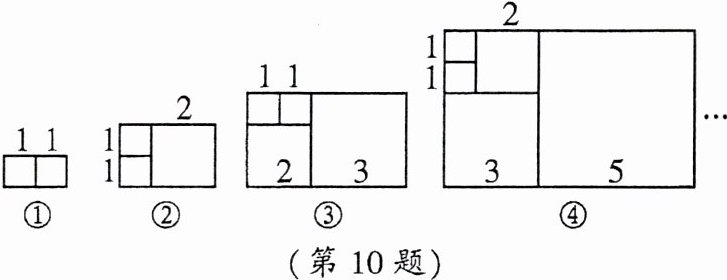
每个长方形的周长如下表所示：
|序号|①|②|③|④|…|
|----|----|----|----|----|----|
|周长|6|10|x|y|…|
(1)仔细观察图形，表中的x= ，y= ；
(2)若按此规律继续拼长方形，则序号为⑩的长方形周长是 。

答案：
(1)16 26
(2)466

11.(1)观察下列图形与等式的关系，并填空：[第11(1)题]
1+3=2²；
1+3+5=3²；
1+3+5+7= ；
1+3+5+7+…+(2n-1)= ；
(2)观察图案，根据(1)中的结论，计算图中黑球的个数，用含有n的代数式填空：[第11(2)题]
1+3+5+…+(2n-1)+( )+(2n-1)+…+5+3+1= 。

答案：
(1)$4^{n}$ $n^{2}$
(2)$2n+1$ $2n^{2}+2n+1$

12.将边长为1的正方形纸片按如图所示方法进行对折，第1次对折后得到的图形面积为S₁，第2次对折后得到的图形面积为S₂，…，第n次对折后得到的图形面积为Sₙ，则S₁+S₂+S₃+…+S₂₀₂₅= 。

答案： $1-\frac {1}{2^{2023}}$

13.毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究：
|名称及几何图形|三角形数|正方形数|五边形数|六边形数|
|----|----|----|----|----|
|层数|点数|点数|点数|点数|
|第1层|1|1|1|1|
|第2层|2|3|4|5|
|第3层|3|5|7|9|
|…|…|…|…|…|
|第6层|▲|▲|▲|▲|
|…|…|…|…|…|
|第n层|▲|▲|▲|▲|
写出第6层各个图形的几何点数，并归纳出第n层各个图形的几何点数。

答案： 6 11 16 21;n $2n-1$ $3n-2$ $4n-3$