《2025年高分突破课时达标讲练测七年级数学上册北师大版》

1.$(-7)^{6}$的意义是( )

A.$-7×6$
B.6个-7相加
C.6个-7相乘
D.7个-6相乘

答案： C

2.(2025·重庆九龙坡区)下列计算正确的是( )

A.$-2^{2}= 4$
B.$(-2)^{2}= 4$
C.$(-2)^{3}= -6$
D.$(-3)^{3}= -9$

答案： B

3.下列各组数中,结果相等的是( )

A.$-|-3|和-(-3)$
B.$-3^{3}和(-3)^{3}$
C.$-3^{2}和(-3)^{2}$
D.$2^{3}和3^{2}$

答案： B

4.若有理数x满足$(x-2)^{2}= 16$,那么有理数x的值为( )

A.6
B.-2
C.6或-2
D.4或-4

答案： C

5.计算:
(1)$(-5)^{3}= $______；
(2)$0.1^{3}= $______；
(3)$-4^{2}= $______；
(4)$-(-3)^{2}= $______；
(5)$(-1\frac{1}{2})^{2}= $______；
(6)$-\frac{(-3)^{3}}{5}= $______。

答案：
(1)-125
(2)0.001
(3)-16
(4)-9
(5)$\frac{9}{4}$
(6)$\frac{27}{5}$

6.(1)已知$(a+2)^{2}+|b-1|= 0$,则$(a+b)^{2025}= $______；
(2)(2025·重庆南开)定义新运算:$x★y= y^{x}-2xy$,例如:$2★3= 3^{2}-2×2×3= -3$,则$3★(-2)= $______。

答案：
(1)-1
(2)4

7.计算:
(1)$(-5)^{3}-3×(-\frac{1}{2})^{4}$；
(2)$(-\frac{3}{4})^{3}+(-\frac{3^{3}}{4})$；
(3)$-1^{100}×(-5)+(-2)^{4}÷4$；
(4)$-1^{4}×2^{3}÷(\frac{4}{9})^{2}×(-\frac{1}{3})^{4}$；
(5)$(-10)^{4}+[(-4)^{2}-(3+3^{2})×2]$。

答案：
(1)$-125\frac{3}{16}$
(2)$-\frac{459}{64}$
(3)9
(4)$-\frac{1}{2}$
(5)9992

8.按如图所示的程序进行运算,若要使输出的结果为40.5,则输入的x值可以是( )


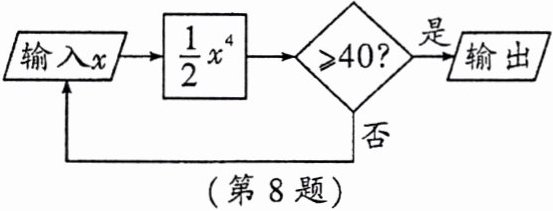
A.2
B.1
C.-2
D.±3

答案： D

9.观察下列等式:$7^{1}= 7$,$7^{2}= 49$,$7^{3}= 343$,$7^{4}= 2401$,$7^{5}= 16807$,…,根据其中的规律可得$7^{1}+7^{2}+…+7^{2025}$的结果的个位数字是( )

A.0
B.1
C.8
D.7

答案： D

10.将一张长方形纸片对折,如图所示可以得到一条折痕MN。继续对折,对折时每次折痕与上次的折痕保持平行,连续对折3次后,可以得到______条折痕,想象一下,如果对折n次,可以得到______条折痕(用含有n的式子表示)。

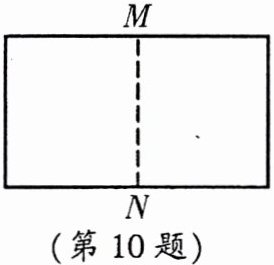
答案： 7 ($2^{7}-1$)