《2025年高分突破课时达标讲练测七年级数学上册北师大版》

10.(2025·成都石室)如图，观察数表，横排为行，竖排为列，根据前五行所表达的规律，说明11/7这个分数位于第 行 列。
第一行 1/1；
第二行 1/2，2/1；
第三行 1/3，2/2，3/1；
第四行 1/4，2/3，3/2，4/1；
第五行 1/5，2/4，3/3，4/2，5/1；
…

答案： 17 11

11.(1)观察一列数a₁=3,a₂=3²,a₃=3³,a₄=3⁴,…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是 ；根据此规律，如果aₙ(n为正整数)表示这列数的第n项，那么a₆= ，aₙ= ；(可用幂的形式表示)
(2)如果想要求1+2+2²+2³+…+2¹⁰的值，可令S₁₀=1+2+2²+2³+…+2¹⁰①，将①式两边同时乘2，得 ②，由②-①，得S₁₀= ；
(3)若(1)中的数共有20项，设S₂₀=3+3²+3³+3⁴+…+3²⁰，请利用上述规律和方法计算S₂₀的值。

答案：
(1)3 $3^{6}$ $3^{n}$
(2)$2S_{10}=2+2^{2}+2^{3}+... +2^{11}$ $2^{11}-1$
(3)$\frac {3^{21}-3}{2}$

12.观察等式：2+2²=2³-2；2+2²+2³=2⁴-2；2+2²+2³+2⁴=2⁵-2；…，已知按一定规律排列的一组数：2⁵⁰,2⁵¹,2⁵²,…,2⁹⁹,2¹⁰⁰。若2⁵⁰=a，用含a的式子表示这组数的和是（ ）

A.2a²-2a
B.2a²-2a-2
C.2a²-a
D.2a²+a

答案： C

13.一种特殊的三角形幻方，是由4个较小的三角形和3个较大的三角形构成的，且满足每个三角形三个顶点处的数之和相等。如图1就是这种特殊的三角形幻方，阴影部分的三角形三个顶点处的数之和为7+3+5=15，该图中每个三角形三个顶点处的数之和都为15。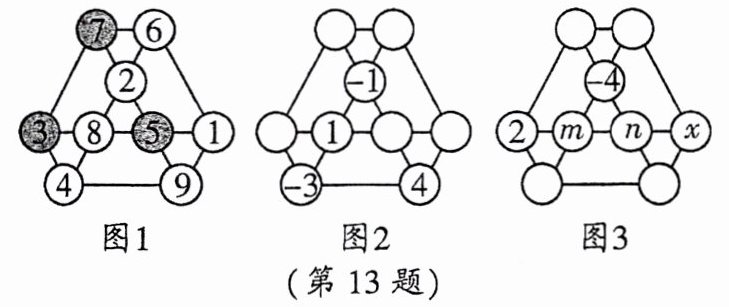
(1)根据图1，计算图中9个数的和与每个三角形三个顶点处的数之和之间的倍数关系，并写出你的结论；
(2)图2也是这种特殊的三角形幻方，请把-4,-2,0,2,3这5个数填在图2的各个圈内；
(3)图3也是这种特殊的三角形幻方，请求x的值。

答案：
(1)图中9个数的和是每个三角形三个顶点处的数之和的三倍
(2)图略
(3)-10