《2025年高分突破课时达标讲练测七年级数学上册北师大版》

9. 请看杨辉三角(如图),并观察下列等式：
$(a+b)^1= a+b$
$(a+b)^2= a^2+2ab+b^2$
$(a+b)^3= a^3+3a^2b+3ab^2+b^3$
$(a+b)^4= a^4+4a^3b+6a^2b^2+4ab^3+b^4$
…
根据前面各式的规律,则$(a+b)^{40}$的第三项系数是______。

答案： 780

10. 有依次排列的3个数：3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串：3,6,9,-1,8,这称为第一次操作；做第二次同样的操作后也产生一个新数串：3,3,6,3,9,-10,-1,9,8,相继依次操作下去,则从数串：3,9,8开始操作第100次时所产生的那个新数串的所有数之和是______。

答案： 520

11. 【观察思考】如图是某同学在棋盘上用围棋摆成的图案。

【规律发现】
(1)第⑤个图案中“•”的个数为______,“○”的个数为______；
(2)第$n$个图案中“•”的个数为______,“○”的个数为______；
【规律应用】
(3)该同学准备用100枚“•”棋子和100枚“○”棋子摆放第$n$个图案,摆放成完整的图案后,写出$n$的最大值为______,此时还剩下______枚棋子。

答案：
(1)15 20
(2)$\frac {n(n+1)}{2}$ 4n
(3)13 57

12. 如图1,在一张白纸上画1条直线,最多能把白纸分成2部分；如图2,在一张白纸上画2条直线,最多能把白纸分成4部分；如图3,在一张白纸上画3条直线,最多能把白纸分成7部分……当在一张白纸上画20条直线,最多能把白纸分成 ( )


A.190部分
B.191部分
C.210部分
D.211部分

答案： D

13. 小明想探究自然数的立方和$1^3+2^3+3^3+…+n^3$(其中$n$为自然数)的推导方法,查阅资料后想到一个方法,把这个代数问题转化为几何问题,具体如下：$1^3$对应图1中边长为1的小正方形个数；$2^3$对应图2中边长为1的小正方形的个数；$3^3$对应图3中边长为1的小正方形的个数。小明发现,图1、图2、图3恰好可以拼成一个边长为6的正方形,从而得到$1^3+2^3+3^3= 36$。

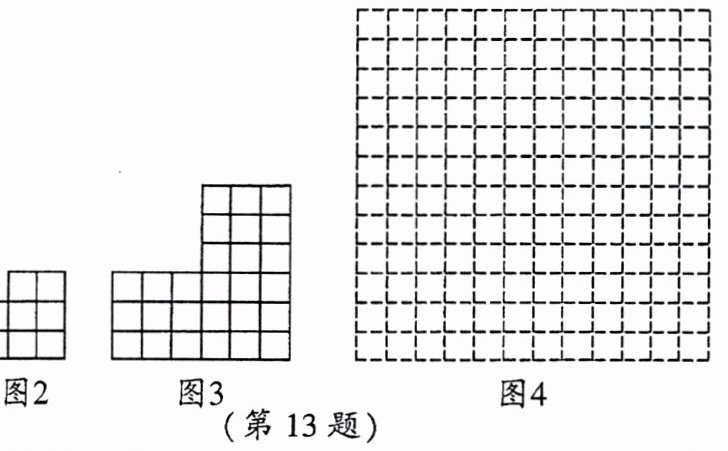
(1)①请你顺着小明的研究思路在图4中画出$4^3$对应的小正方形个数的摆放图形；
②把这4个图形拼成一个正方形,则这个正方形的边长为______；
(2)根据小明的发现,请直接写出$1^3+2^3+3^3+…+n^3= $______(用含$n$的式子表示)；
(3)请根据第(2)问的规律求$20^3+21^3+22^3+…+100^3$的值。

答案：
(1)①图略 ②10
(2)$\frac {n^{2}(n+1)^{2}}{4}$
(3)25 466 400